Question 1: Determine whether each of the following is a convex program. Justify your answer.
Question 2: A trucking company specializes in transporting hazardous materials. Due to the nature of its business, the company places great importance on maintaining a clean driving safety record. This not only helps keep its reputation up, but it also helps keep its insurance premiums down. The company is also conscious of the fact that when carrying hazardous materials, the environmental consequences of even a minor accident could be disastrous. Taking this into account, the company is trying to ensure the selection of routes that are least likely to result in an accident.
Currently, the company wants to identify the safest routes for carrying a load of hazardous materials from Los Angeles, California, to Amarillo, Texas. The network below summarizes the legs under consideration, where the number on each arc represents the probability of having an accident on each potential leg of the journey. Note that a route is made up of several legs starting at the load's origin and ending at its destination.
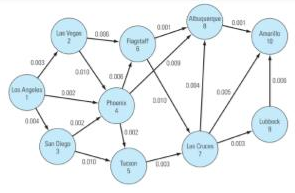
i) Provide an algebraic formulation for determining the route that minimizes the probability of having an accident, while assuming independence of accidents occurring on any leg. (Hint: It is easier to think of the equivalent objective of maximizing the probability of having no accident).
ii) Implement and solve the model in Excel. Report the solution.
iii) A log-concave function, f(x) > 0, is one whose logarithm, log(f(x)), is concave. Note that since log(x) is monotonically increasing in x > 0, then f(x2) > f(x1) ⇔ log(f(x2)) > log(f(x1)). Accordingly, if log(f(x)), f(x) > 0, is concave and, hence, has a unique maximum, then f(x) itself must be uni-modal and possessing a unique maximum as well (but f(x) does not have to be concave). With this background, establish that the optimal solution obtained for this model is always a global maximum.
Question 3: Consider the following quadratic program (QP).
maximize -(x1)2 -8(x2)2 - 2(x3)2 + 10x2x3 + 14x1 - 8x2 + 20x3
subject to: x1 + 4x3 = 4
-x2 + 3x3 = 1
a. A general symmetric quadratic program can be stated as:
max cTx + xTQx
s.t.: Ax = b
What are the values for Q. c, A and b for this QP?
b. Write the KKT conditions for the model.
c. Solve the system of equations from (b) to find the KKT point for the model.
d. Is the point you obtained in (c) a global optimum for the QP? Clearly justify your answer.
Question 4: Each day q1 tons of freight arrive by sea in Japan bound for in-country regions i = 1 . . . , 150. These goods may arrive at any of the major ports j = 1,. . . , 17, but the internal transportation cost per ton cij varies by port and destination. The government plans a capital investment program in port facilities to secure a daily tonnage processing capacity at each port j that minimize the total transportation, maintenance and delay costs. Port j's maintenance costs can be expressed as aj, (capacity of port j)b_1 , where aj (> 0) and bj (> I) are known constants. Delay cost at j can be estimated by d/[( capacity of port j)-( tons shipped through port j)], where d is the delay cost per ton per day. In order to avoid singularities due to the delay cost expression, it is required, for modeling purposes, that the tons shipped through a port do not exceed 99% of the port's capacity. Formulate an NLP model to optimize the ports using the decision variables (i = 1, . . . , 150, j = 1, . . . , 17):
xij 
tons shipped through port j for region i ,
xj tons shipped through port j , and
yj capacity of port j.
a. Provide a complete algebraic formulation for the problem.
b. Attempt to determine if your formulation corresponds to a convex program or not.
Get in touch with our Convex Program Assignment Help service and get benefitted in your academic success. By availing our online service, you will get the most authentic and faultless assignment paper.
Tags: Convex Program Assignment Help, Convex Program Homework Help, Convex Program Coursework, Maximizing Probability Assignment Help, Maximizing Probability Homework Help, Minimizing Probability Assignment Help, Minimizing Probability Homework Help, Quadratic Program Assignment Help, Quadratic Program Homework Help, Quadratic Program Solved Assignments