A support bar will be in equilibrium (or balanced) at the fulcrum, O, if m1x + m2y = m3z, where m1, m2 and m3 symbolize masses and x, y and z signify the distance of the masses to the fulcrum. Draw a diagram for each question and compute the answer.
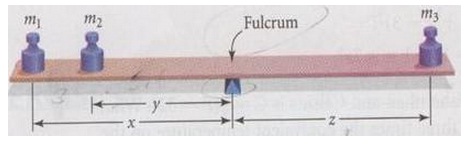
Q1. A 40 in. bar is in equilibrium if a weight of 6lb is hung from one end and a weight of 9lb is hung from the other end. Determine the position of fulcrum.
Q2. While in the park, Michael and his two sons, Alden and Justin, go on a 16ft see-saw. Michael, who weighs 150lb, sits at edge of one end while the Justin and Alden move to the other side and try to balance. The see-saw balances with Justin at the other edge and Alden 3ft from him. After some extra experimentation the see-saw balances once again with Alden at the edge and Justin 5.6ft from the fulcrum. How much does each of the boy weigh?