Determining outputs to form the decision variable

Question

Solve the following problem:

Suppose that the binary signal ±sl(t) is transmitted over a fading channel and the received signal is

r₁(t) = ±as₁(t) + z(t), 0 ≤ t ≤ T

where z(t) is zero-mean white Gaussian noise with autocorrelation function

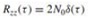
The energy in the transmitted signal is ε = 1/2 ∫^T₀ |s₁(t)|² dt .The channel gain α is specified by the probability density function
p(α) = 0.1δ(α) + 0.9δ(α - 2)

a. Determine the average probability of error P_b for the demodulator that employs a filter matched to s₁(t).

b. What value does P_b approach as E/N₀ approaches infinity?

c. Suppose that the same signal is transmitted on two statistically independently fading channels with gains a₁ and a₂, where

p(α_k) = 0.1δ(α_k) + 0.9δ(α_k - 2),    k= 1,2

The noises on the two channels are statistically independent and identically distributed. The demodulator employs a matched filter for each channel and simply adds the two filter outputs to form the decision variable. Determine the average P_b.

d. For the case in (c) what value does P_b approach as E/N₀ approaches infinity?