Assignment:
Q1. You have been asked to determine the least expensive route for a telephone cable that connects Andersonville with Beantown (see figure below)
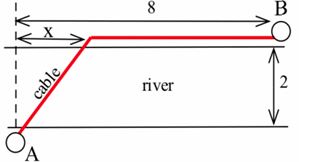
If it costs $5000 per mile to lay the cable on land and $8000 per mile to lay the cable acrossthe river (with the cost of the cable included), find the least expensive route.
Q2. Find the shortest distance from the point (2, 0) tothe curve:
Y=3x-1
y=x^2
x^2+y^2=1
Y=sin(x)
Q3. Find the dimensions of the rectangle with thegreatest area that can be built so the base ofthe rectangle is on the x-axis between 0 and 1and one corner of the rectangle is on the curve
y=x^3. What is the area of this rectangle?
Q4. Calculate the limit of each expression as "x→ ∞."
(7x+12)/(3x-2)
Q5. same instructions as Q4
(x+sin?(x))/(x-sin?(x) )
Provide complete and step by step solution for the question and show calculations and use formulas.