Assignment:
Question 1. When a high-speed passenger train traveling at 161 km/h rounds a bend, the engineer is shocked to see that a locomotive has improperly entered onto the track from a siding and is a distance D=676m ahead. The locomotive is moving at 29 km/h. The engineer of the high speed train immediately applies the brakes. For a collision to be just avoided, what must be the deceleration of the passenger train?
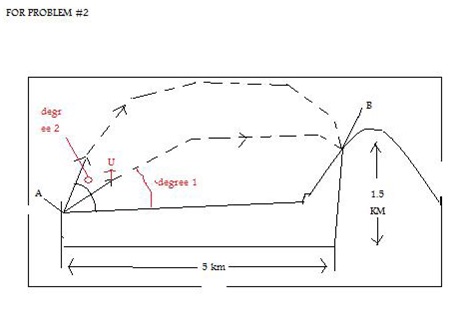
Question 2. The muzzle velocity of a long range rifle at A is u=400 m/s. Determine the two angles of elevation ( degree 1 and degree 2) which will permit the projectile to hit the mountain target B. (Hint: Solve the equation X=Voxt for t and substitute into the equation for y (t). Express the two initial velocity components Vox and Voy in terms of degree. You then have the equation of the parabola: y=y (x). Use the trig identity (1/cos^2 degree) = tan ^2 degree + 1 as well as the values of x and y at point B to obtain a quadratic equation for tan degree. Solve using the quadratic formula for the two roots (two values of tan degree) and hence the two values of degree.)