Determining-applications of linear equations

Question

Questions:

1A: Applications of Linear Equations

1. Joe has a collection of nickels and dimes that is worth $5.65. If the number of dimes were doubled and the number of nickels were increased by 8, the value of the coins would be $10.45. How many dimes does he have?
2. An express and local train leave Gray's Lake at 3 P.M. and head for Chicago 50 miles away. The express travels twice as fast as the local, and arrives 1 hour ahead of it. Find the speed of each train.
3. Walt made an extra $9000 last year from a part-time job. He invested part of the money at 9% and the rest at 8%. He made a total of $770 in interest. How much was invested at 8%?

1B: Discussion Questions

1. How many solutions exist for a quadratic equation?  How do we determine whether the solutions are real or complex?

2. What three techniques can be used to solve a quadratic equation?  Demonstrate these techniques on the equation "12x² - 10x - 42 = 0".

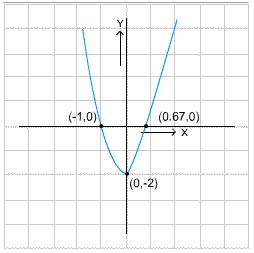
3. Look at the graph above and comment on the sign of D or the discriminant. Form the quadratic equation based on the information provided and find its solution.

4. Translate the following into a quadratic equation, and solve it:  The length of a rectangular garden is three times its width; if the area of the garden is 75 square meters, what are its dimensions?

1C: Solutions of Quadratic Equations and their Applications

1. Determine whether the following equations have a solution or not? Justify your answer.

a)x² + 6x - 7 = 0

b)z² + z + 1 = 0

c)(3)^1/2y² - 4y - 7(3)^1/2 = 0

d)2x² - 10x + 25 = 0

e)2x² - 6x + 5 = 0

f) s² - 4s + 4 = 0

g)5/6x² - 7x - 6/5 = 0

h)7a² + 8a + 2 = 0

1. If x = 1 and x = -8, then form a quadratic equation.
2. What type of solution do you get for quadratic equations where D < 0? Give reasons for your answer. Also provide an example of such a quadratic equation and find the solution of the equation.
3. Create a real-life situation that fits into the equation (x + 4)(x - 7) = 0 and express the situation as the same equation.

1D: Practical Application of Quadratic Equations

1. A rectangular garden has dimensions of 18 feet by 13 feet. A gravel path of uniform width is to be built around the garden. How wide can the path be if there is enough gravel for 516 square feet?
2. A business invests $10,000 in a savings account for two years.  At the beginning of the second year, an additional $3500 is invested.  At the end of the second year, the account balance is $15,569.75.  What was the annual interest rate?
3. Steve traveled 200 miles at a certain speed. Had he gone 10mph faster, the trip would have taken 1 hour less. Find the speed of his vehicle.
4. The Hudson River flows at a rate of 3 miles per hour.  A patrol boat travels 60 miles upriver, and returns in a total time of 9 hours.  What is the speed of the boat in still water?

1E: Discussion Questions - 5(1B)

1.  
   1.  Do exponential functions only model phenomena that grow, or can they also model phenomena that decay?  Explain what is different in the form of the function in each case.
   2.  True or false: The function "f(x) = 3^x" grows three times faster than the function "g(x) = x".  Explain.
   3. What are the asymptotes of the functions "f(x) = 3^x" and "g(x) = log₅2x"?

4. A cell divides into two identical copies every 4 minutes.  How many cells will exist after 3 hours?

5. The level of thorium in a sample decreases by a factor of one-half every 4.2 million years.  A meteorite is discovered to have only 7.6% of its original thorium remaining.  How old is the meteorite?

1F: Assignment 3: Graphs of Exponential and Logarithmic Functions

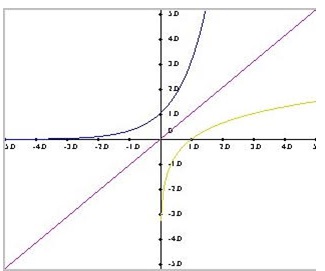
Refer to the graph given below and identify the graph that represents the corresponding function. Justify your answer.
y = 3^x
y = log₃x

Plot the graphs of the following functions. Scan the graphs and post them to the Facilitator along with your response.

1. f(x)=7^x

2. f(x)=4^{x - 3}

3. f(x)=(1/5)^x

4. f(x)= log₃x

1G: Discussion Questions

1. Give an example of an exponential function. Convert this exponential function to a logarithmic function. Plot the graph of both the functions and post to the discussion forum. Discuss these functions and their graphs with your classmates.

1. Form each of the following:

• A linear equation in one variable
• A linear equation in two variables
• A quadratic equation
• A polynomial of three terms
• An exponential function
• A logarithmic function

1. Plot the graph of the above equations formed in question 2, and post your response to the discussion forum.

1. Derive the quadratic and linear equations from the corresponding graphs of a classmate.

Plot the graphs of the following functions. Scan the graphs and post them to the Facilitator along with your response.

1 f(x)=7^x

2(x)=4^{x - 3}

3(x)=(1/5)^x

4(x)= log₃x

1H: Evaluate Functions

Evaluate the functions for the values of x given as 1, 2, 4, 8, and 16. Describe the differences in the rate at which each function changes with increasing values of x.

1. f(x) = 5x - 3
2. f(x) = x² - 3x + 2
3. f(x) = 2x³ + 7x² - x - 1
4. f(x) = 10^x
5. f(x) = ln x