Determine the wavelength of the monochromatic light

Question

Assignment:

Part 1

• Demonstrate that the minimum distance possible between a real object and its real image through a thin convex lens is 4f, where f is the focal length of the lens.

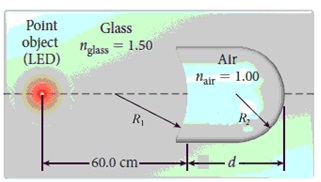
• An air-filled cavity bound by two spherical surfaces is created inside a glass block. The two spherical surfaces have radii R₁ = 34.4 cm and R₂ = 21.0 cm, respectively, and the thickness of the cavity is d = 41.2 cm (see diagram below). A light-emitting diode (LED) is embedded inside the block a distance of 60.0 cm in front of the cavity. Given n_glass = 1.50 and n_air = 1.00, and using only paraxial light rays (i.e., in the paraxial approximation) do the following. (The paraxial approximation is a small angle approximation so sin(θ) ≈ θ. This applies to both the incident angles and refracted angles.) (a) Calculate the final position of the image of the LED through the air-filled cavity. (b) Draw a ray diagram showing how the image is formed.

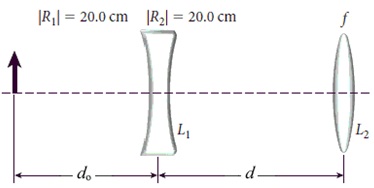
• Two lenses are used to create an image for a source 10.0 cm tall that is located at do = 31.0 cm to the left of the first lens, as shown in the figure below. Lens L₁ is a biconcave lens made of crown glass (index of refraction n = 1.55) and has a radius of curvature of 20.0 cm for both surface 1 and 2. Lens L₂ is d = 39.0 cm to the right of the first lens L₁. Lens L2 is a converging lens with a focal length f = 30.5 cm. At what distance relative to the object does the image get formed? Determine this position by sketching rays and calculating algebraically.

• Some reflecting telescope mirrors utilize a rotating tub of mercury to produce a large parabolic surface. If the tub is rotating on its axis with an angular frequency ω, show that the focal length of the resulting mirror is: f = g/2ω².

• Jack has a near point of 30.2 cm and uses a magnifier of 27.0 diopter. (a) What is the magnification if the final image is at infinity? (b) What is the magnification if the final image is at the near point?

• A diverging lens with f = -28.0 cm is placed 16.1 cm behind a converging lens with f = 21.6 cm. Where will an object at infinity in front of the converging lens be focused?

Part 2

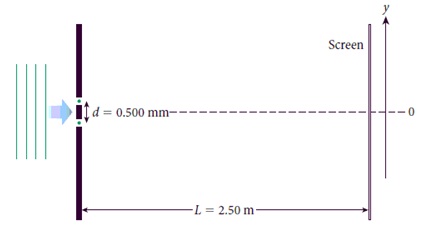
1- Coherent monochromatic light with wavelength λ = 530 nm is incident on two slits that are separated by a distance d = 0.500 mm. The intensity of the radiation at a screen 2.50 m away from each slit is 168.0 W/cm². Determine the position y1/3 at which the intensity of the central peak (at y = 0) drops to Imax/3.

• White light (400 nm < λ < 750 nm) shines onto a puddle of water (n = 1.33). There is a thin (109.7 nm thick) layer of oil (n = 1.47) on top of the water. What wavelengths of light would you see reflected?

• Some mirrors for infrared lasers are constructed with alternating layers of hafnia and silica. Suppose you want to produce constructive interference from a thin film of hafnia (n = 1.90) on BK-7 glass (n = 1.51) when infrared radiation of wavelength 1.39 µm is used. What is the smallest film thickness that would be appropriate, assuming the laser beam is oriented at right angles to the film?

• Sometimes thin films are used as filters to prevent certain colors from entering a lens. Consider an infrared filter, designed to prevent 847.0-nm light from entering a lens. Find the minimum film thickness for a layer of MgF₂ (n = 1.38) to prevent this light from entering the lens.

• White light shines on a sheet of a material that has a uniform thickness of 1.44 µm. When the reflected light is viewed using a spectrometer, it is noted that light with wavelengths of 499.2 nm, 561.6 nm, 641.8 nm, 748.8 nm, and 898.6 nm is not present in the reflected light. What is the index of refraction of the material?

• A common interference setup consists of a plano-convex lens placed on a plane mirror and illuminated from above at normal incidence with monochromatic light. The pattern of circular interference fringes (fringes of equal thickness)-bright and dark circles-formed due to the air wedge defined by the two glass surfaces, is known as Newton's rings. In an experiment using a plano-convex lens with focal length f = 80.50 cm and index of refraction nl = 1.500, the radius of the third bright circle is found to be 0.8525 mm. Determine the wavelength of the monochromatic light.

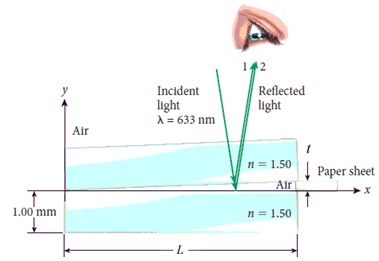
• A single beam of coherent light (λ = 633 • 10-9 m) is incident on two glass slides, which are touching at one end and are separated by a t = 0.0275-mm thick sheet of paper on the other end, as shown in the figure below. Beam 1 reflects off the bottom surface of the top slide, and Beam 2 reflects of the top surface of the bottom slide. Assume that all the beams are perfectly vertical and that they are perpendicular to both slides, i.e., the slides are nearly parallel (the angle is exaggerated in the figure); the beams are shown at angles in the figure so that they are easier to identify. Beams 1 and 2 recombine at the location of the eye in the figure below. The slides are L = 7.20 cm long. Starting from the left end (x = 0) at what positions xbright do bright bands appear to the observer above the slides?