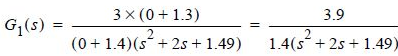Solved: Determine the system impulse response in time domain and, Electrical Engineering

+44 141 628 6080
[email protected]

Determine the system impulse response in time domain and

Physical system modeling, time response and stability

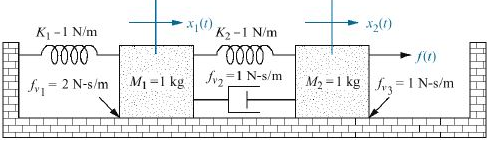
60_Physical system modeling.png

1. Find the differential equations relating input force f(t) and output displacement x₁(t) and x₂(t) in the system.

(Hint: K, f_v and M are spring constant, friction coefficient and mass respectively)

2. Determine the transfer function G(s)=X₁(s)/F(s). For the following suppose G(s) = 3 x s+ 13/(s + 1.4)(s² + 2s + 1.49)

3. Determine the system impulse response in time domain.

4. Draw its root locus and comment on system stability.

5. If the system can be simplified using the system dominant pole technique into G₁(s) below, obtain the system response for a unit step input, and estimate the overshot and settling time.

View Complete Question

Solution Preview :

Prepared by a verified Expert

Electrical Engineering: Determine the system impulse response in time domain and

Reference No:- TGS0583128

Now Priced at $40 (50% Discount)

Recommended (96%)

Rated (4.8/5)

Have a Question? (oR Write a Review)

Write atleast 100 words!!

Recent Questions Asked Electrical Engineering

Q : Imagine that there are 1000 consumers who have preferences

Imagine that there are 1,000 consumers who have preferences consistent with the same quasi-linear utility function (ui[x1; x2] = 10 ln[x1] + 10x2, which impliesMRS = ). (a) Sketch the individual consumer's demand curve for good1.

Q : The first amendment does not guarantee absolute freedoms or

The First Amendment does not guarantee absolute freedoms or rights Why?

Q : A car is stopped for a traffic signal when the light turns

A car is stopped for a traffic signal. When the light turns green, the car accelerates, increasing its speed from 0 to 5.80 m/s, What is the magnitude of the linear impulse experienced by a 74.0-kg passenger in the car during the time the car acceler

Q : List the four major cultural regions in afro-eurasia and

List the four major cultural regions in Afro-Eurasia, and briefly explain the defining characteristics of each. What did the various people and groups in these geographic areas all have in common that distinguished them from others?"

Q : Determine the system impulse response in time domain and

Determine the system impulse response in time domain and draw its root locus and comment on system stability.

Q : Recall the espresso machinecontribution game discussed in

Recall the espresso machinecontribution game discussed in class. You and your roommate may by an espresso machine for $50. Your value for havingthe espresso machine is $40 and your value for not having it is zero.

Q : How much heat is produced in burning 8 mol of ch4 under

How much heat is produced in burning 8 mol of CH4 under standard conditions if reactants and products are brought to 298 and H2 O(l) is formed. What is the maximum amount of useful work that can be accomplished under standard conditions by this sy

Q : You have two parallel wires with current flowing in

You have two parallel wires with current flowing in opposite directions, If each current is 2A, and the distance between the two wires is 0.5m, what is the force per meter between the wires

Q : Would you expect cobaltiii acetylacetonate to be a

Would you expect Cobalt(III) Acetylacetonate to be a diamagnetic or paramagnetic compound

1925200

Questions
Asked

3,689

Active Tutors

1414730

Questions
Answered

Start Excelling in your courses, Ask a tutor for help and get answers for your problems !!

ask Question

Solution Preview :

Prepared by a verified Expert

Electrical Engineering: Determine the system impulse response in time domain and

Reference No:- TGS0583128

Have a Question? (oR Write a Review)

Recent Questions Asked Electrical Engineering

Q : Imagine that there are 1000 consumers who have preferences

Q : The first amendment does not guarantee absolute freedoms or

Q : A car is stopped for a traffic signal when the light turns

Q : List the four major cultural regions in afro-eurasia and

Q : Determine the system impulse response in time domain and

Q : Recall the espresso machinecontribution game discussed in

Q : How much heat is produced in burning 8 mol of ch4 under

Q : You have two parallel wires with current flowing in

Q : Would you expect cobaltiii acetylacetonate to be a

How sociological models help understand mental illness

Statement about political systems controlled by men

What when people get involved in community and social change

Compare critical feminist theory and power-control theory

Which are forms of media bias

Identify problems and concerns that contributed

Which of the things happened first

Solution Preview :

Prepared by a verified Expert

Electrical Engineering: Determine the system impulse response in time domain and

Reference No:- TGS0583128

Recent Questions Asked Electrical Engineering

Q : Imagine that there are 1000 consumers who have preferences

Q : The first amendment does not guarantee absolute freedoms or

Q : A car is stopped for a traffic signal when the light turns

Q : List the four major cultural regions in afro-eurasia and

Q : Determine the system impulse response in time domain and

Q : Recall the espresso machinecontribution game discussed in

Q : How much heat is produced in burning 8 mol of ch4 under

Q : You have two parallel wires with current flowing in

Q : Would you expect cobaltiii acetylacetonate to be a

Asked Questions