Solve the following problem:
The block diagram of a two-path communication system is shown in Figure . In the first path noise n1(t) is added to the transmitted signal. In the second path the signal is subject to a random amplification A and additive noise n2(t). The random variable A takes values ±1 with equal probability. The transmitted signal is binary antipodal, and the two messages are equiprobable. Both n1(t) and n2(t) are zero-mean, white, Gaussian noise processes with power spectral densities N1/2 and N2/2, respectively. The receiver observes both r1(t) and r2(t).
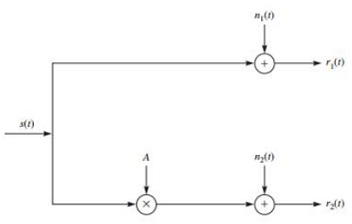
1. Assuming that the two noise processes are independent, determine the structure of the optimum receiver and find an expression for the error probability.
2. Now assume N1 = N2 = 2 and E[n1n2] = 1/2, where n1 and n2 denote the projections of n1(t) and n2(t) on the unit signal in the direction of s(t) (obviously the two noise processes are dependent). Determine the structure of the optimum receiver in this case.
3. What is the structure of the optimal receiver if the noise processes are independent and the receiver has access to r(t) = r1(t) + r2(t) instead of observing r1(t) and r2(t) separately?
4. Determine the optimal decision rule if the two noise processes are independent and A can take 0 and 1 with equal probability [receiver has access to both r1(t) and r2(t)].
5. What is the optimal detection rule in part 4 if we assume that the upper link is similar to the lower link but with A substituted with random variable B where B = 1 - A (the lower link remains unchanged)?