Assignment:
1. A machine has the first cost of $60K. The net annual savings (which depends on the volume of throughput) and the salvage value at the end of its 8-year economic life (which depends on the progress in related technology) are given below:
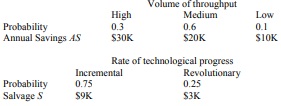
Assume that the progress in technology and the level of throughput volume are independent, and MARR is 10%.
a) Write the probability distribution of EAW, then compute the expected EAW, the standard deviation of EAW and the probability the there will be a loss in this investment. You may first write down the following formula:
EAW(10%) =
Then fill in the following table: (Note: (A/P, 10%, 8) = 0.1874; (A/F, 10%, 8) = 0.0874)
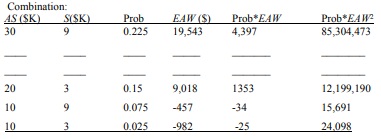
E(EAW) =_________________
SD(EAW) =_________________
b) Is this a good investment based on your own return/risk trade-off? Why or why not? If the distribution of PW is approximately normal, what is the probability of loss? (Table of Standard Normal distribution is given.)
2. A new device is being purchase for a certain project in a local community. The following financial parameters have been estimated:
Intital Cost $100,000
Annual savings (AS) $20,000
Useful life (N) 10 years
Salvage value (end of 10 years) $30,000
MARR (annual) 10%
There is considerable uncertainty surrounding the estimates of annual savings--- between -20% and +25%, and useful life---7 years to 12 years.
a) Construct the best and worst scenarios
b) Draw a spider plot (PW v.s. %), and conclude whether any of the two is sensitive, and which of the two is more sensitive. First compute the following: (Interest Table for 10% is given)
Nominal PW = -100K+ 30K*(P/F,10%,10) +20K*(P/A,10%,10) =$34,458
PW(AS=80% )= -100K+30K*(P/F,10%,10)+16K*(P/A,10%,10) =$9,879
PW(AS=125% )= -100K+30K*(P/F,10%,10)+25K*(P/A,10%,10) =$65,180
PW(N=70% )= -100K+30K*(P/F,10%,___)+20K*(P/A,10%,___) =___
PW(N=120% )= -100K+30K*(P/F,10%,___)+20K*(P/A,10%,___) =___
Then draw the spider plot and determine whether (i) PW is sensitive to either parameter and (ii) the decision is sensitive to either parameter
c) Suppose we know that AS is distributed as a triangular distribution with the minimum value = $16K, the most likely value = $20K and the maximum value = $25K. Suppose we also know that integer N is uniformly distributed between 7 years to 12 years. Use the following independent uniform random number series to generate 5 scenarios (i.e. 5 replications of AS using the first series beginning from left, and 5 replications of N using the second series beginning from left also). Then compute PW at 10% MARR under the five simulated scenarios and the average PW. Compare this with the nominal PW in part (c) and comment Uniform random numbers to generate AS and N (begin from left to right):
Series 1: 0.2350 0.9043 0.0418 0.7504 0.1237 0.4578 0.9887 0.7681 0.0348 0.5612...
Series 2: 0.0965 0.9665 0.6484 0.4922 0.4950 0.1014 0.4845 0.2350 0.9043 0.0418...
Scenario: AS N PW
1 ____ ___ ____
2 ____ ___ ____
3 ____ ___ ____
4 ____ ___ ____
5 ____ ___ ____
Average PW ____
3. Crain Energy announced that it has discovered oil in an oil exploration well in Northwestern India. Initial estimates placed the find between 50 million and 200 million barrels of recoverable oil. To extract the oil, there is a $400M investment in the field and a $50M remediation cost at the end of the project. Regardless of the size of the reserve, the net annual revenue of $66M per year can be expected.
However, at the constant extraction rate of 10,000 barrels per day, the smaller reserve will last 14 years, while the larger reserve 56 years. The chance of hitting a large reserve is 60% and the chance of hitting a small reserve is 40%. Assume the interest rate is 15%. Before making the initial investment to extract oil, Crain Energy has the option of digging an appraisal well and performs additional seismic testing to better understand the amount of reserves. Assume that the testing can be characterized as "Favorable---F" or "Unfavorable---UF". More important we know that the test will predict "Favorable" if it is actually large 90% of the time, and it will predict "Unfavorable" if the well is actually small 80% of the time.
The corresponding decision tree is as follows:
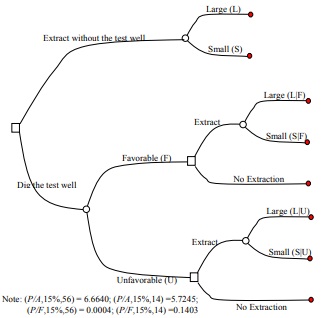
The following computations provide the necessary conditional, marginal and other probabilities. Fill in the missing entries
Testing Result Prior Joint probability
Favorable F Unfavorable U Probability Favorable F Unfavorable U
Large reserve (L) 0.90 0.10 0.60 0.54 .......
Small reserve (S) 0.20 0.80 0.40 ...... 0.32
...... ..... Marginal Pr
Pr(F) Pr(U)
Large reserve (L) Pr(L|F) ...... ...... P(L|U)
Small reserve (S) Pr(S|F) ...... ...... P(S|U)
a) Write down all cash flows and probabilities on the tree. Then perform all the necessary roll-back calculations on the decision tree.
b) If the test costs $1M, what would be your optimal strategy?
c) What is the maximum worth of the test (i.e. find EVSI)? And also, what is the value of perfect information (EVPI)?