Determine the power spectral density of transmitted signal

Question

Solve the following problem:

Consider the signal constellation shown in Figure

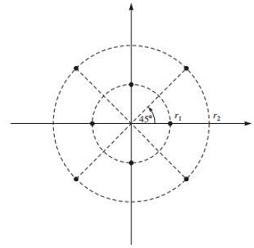
The lowpass equivalent of the transmitted signal is represented as

           ∞
s₁(t) = Σ  a_ng(t - nT)
        n=-∞

where g(t) is a rectangular pulse defined as

g(t) = {1    0≤t          {0    otherwise

and the an's are independent and identically distributed (iid) random variables that can assume the points in the constellation with equal probability.

1. Determine the power spectral density of the signal s₁(t).

2. Determine the power spectral density of the transmitted signal s(t), assuming that the carrier frequency is f₀ (assuming f0 >> 1/T ).

3. Determine and plot the power spectral density of s₁(t) for the case when r₁ = r₂ (plot the PSD as a function of f T ).