Question 1:
The dimensions of a badminton court are as shown below in plan view.
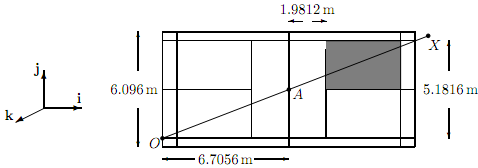
A player at the point O smashes the shuttlecock from a point Y at a height of 3.00m vertically above O. Assume that the shuttlecock then travels in a straight line directly over the net at the midpoint A, which is at a height of 1.55m, before bouncing at the point X. The unit vector k is directed vertically upwards.
(a) Taking the origin at O and axes as shown in the figure, write down the position vectors of the points Y and A. [2]
(b) Determine the position vector of any point on the line Y A, and hence find the position vector of the point X. Deduce that the shuttlecock cannot land in the shaded area of the court.
(c) Find the distance travelled by the shuttlecock between the point of the smash and hitting the floor.
(d) Find the dot product of the vectors XO→ and XY→ , and hence determine the angle below the horizontal at which the shuttlecock travels before landing. Give your answer in degrees correct to two decimal places.
(e) Find the cross product of the vectors YX→ and YO→, and use this result to determine the area of the triangle OY X and a unit vector perpendicular to YX→ and YO→.
Question 2
Consider the vector v shown in the following diagram.
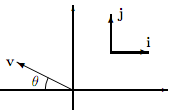
Find the i- and j-components of v in terms of the magnitude of v and θ, simplifying your answers as far as possible.