ADES, INC. CASE
Response to the following problem:
Use of Currency Derivative Instruments
Blades, Inc., needs to order supplies 2 months ahead of the delivery date. It is considering an order from a Japanese supplier that requires a payment of 12.5 million yen payable as of the delivery date. Blades has two choices:
¦ Purchase two call options contracts (since each option contract represents 6,250,000 yen).
¦ Purchase one futures contract (which represents 12.5 million yen). The futures price on yen has historically exhibited a slight discount from the existing spot rate. However, the firm would like to use currency options to hedge payables in Japanese yen for transactions 2 months in advance. Blades would prefer hedging its yen payable position because it is uncomfortable leaving the position open given the historical volatility of the yen. Nevertheless, the firm would be willing to remain unhedged if the yen becomes more stable someday. Ben Holt, Blades' chief financial officer (CFO), prefers the flexibility that options offer over forward contracts or futures contracts because he can let the options expire if the yen depreciates. He would like to use an exercise price that is about 5 percent above the existing spot rate to ensure that Blades will have to pay no more than 5 percent above the existing spot rate for a transaction 2 months beyond its order date, as long as the option premium is no more than 1.6 percent of the price it would have to pay per unit when exercising the option. In general, options on the yen have required a premium of about 1.5 percent of the total transaction amount that would be paid if the option is exercised. For example, recently the yen spot rate was $.0072, and the firm purchased a call option with an exercise price of $.00756, which is 5 percent above the existing spot rate. The premium for this option was $.0001134, which is 1.5 percent of the price to be paid per yen if the option is exercised. A recent event caused more uncertainty about the yen's future value, although it did not affect the spot rate or the forward or futures rate of the yen. Specifically, the yen's spot rate was still $.0072, but the option premium for a call option with an exercise price of $.00756 was now $.0001512. An alternative call option is available with an expiration date of 2 months from now; it has a premium of $.0001134 (which is the size of the premium that would have existed for the option desired before the event), but it is for a call option with an exercise price of $.00792The table below summarizes the option and futures information available to Blades:
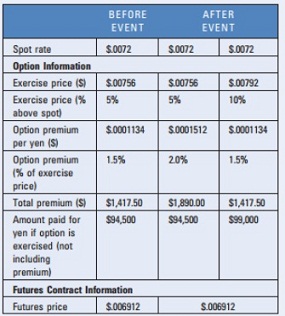
As an analyst for Blades, you have been asked to offer insight on how to hedge. Use a spreadsheet to support your analysis of questions 4 and 6
1. If Blades uses call options to hedge its yen payables, should it use the call option with the exercise price of $.00756 or the call option with the exercise price of $.00792? Describe the tradeoff.
2. Should Blades allow its yen position to be unhedged? Describe the tradeoff.
3. Assume there are speculators who attempt to capitalize on their expectation of the yen's movement over the 2 months between the order and delivery dates by either buying or selling yen futures now and buying or selling yen at the future spot rate. Given this information, what is the expectation on the order date of the yen spot rate by the delivery date? (Your answer should consist of one number.)
4. Assume that the firm shares the market consensus of the future yen spot rate. Given this expectation and given that the firm makes a decision (i.e., option, futures contract, remain unhedged) purely on a cost basis, what would be its optimal choice?
5. Will the choice you made as to the optimal hedging strategy in question 4 definitely turn out to be the lowest-cost alternative in terms of actual costs incurred? Why or why not?
6. Now assume that you have determined that the historical standard deviation of the yen is about $.0005. Based on your assessment, you believe it is highly unlikely that the future spot rate will be more than two standard deviations above the expected spot rate by the delivery date. Also assume that the futures price remains at its current level of $.006912. Based on this expectation of the future spot rate, what is the optimal hedge for the firm?