Determine the optimal decision rule for the receiver

Question

Solve the following problem:

A communication system employs M signals for {sm(t)}^M_m=1  transmission of M equiprobable messages. The receiver has two antennas and receives two signals r₁(t) = s_m(t) + n₁(t) and r₂(t) = s_m(t) + n₂(t) by these antennas. Both n₁(t) and n₂(t) are white Gaussian noises with power spectral densities N₀1/2 and N02/2, respectively. The receiver makes its optimal detection based on the observation of both r1(t) and r₂(t). It is further assumed that the two noise processes are independent

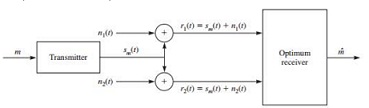
1. Determine the optimal decision rule for this receiver.

2. Assuming N₀1 = N₀2 = N₀, determine the optimal receiver structure.

3. Show that under the assumption of part 2, the receiver needs to know only r₁(t)+r₂(t).

4. Now assume the system is binary and employs on-off signaling (i.e., s₁(t) = s(t) and s₂(t) = 0), and show that the optimal decision rule consists of comparing r₁ +αr₂ with a threshold. Determine α and the threshold (in this part you are assuming noise powers are different).

5. Show that in part 4, if noise powers are equal, then α = 1, and determine the error probability in this case. How does this system compare with a system that has only one antenna, i.e., receives only r₁(t)?