1. Determine the maximum likelihood estimator for μ from an exponential random sample X1, . . . ,XN with common mean EX1 = μ. Make sure to verify that your estimator indeed maximises the likelihood.
2. Determine an exact 1 -α� stochastic con�dence interval for λ based on an exponential random sample X1, . . . ,XN ~ ∈iid Exp(λ).
3. Give an appropriate test-statistic T, its distribution under H0, and a critical region C� for the two-sided hypothesis test H0, λ = λ0 vs H1. λ = λ0, assuming under H0 that data is distributed as X1, . . . ,XN ~ ∈iid Exp(λ0).
4. The least-squares solution β^ for a linear regression model is β^= (β^ 0, β^1 )T , where
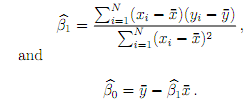
Verify that β^ solves the normal equations ATAβ � = ATy for data y.
5. For an outcome Y = y of a linear model Y = Aβ� + ∈ ", where " ∈ ~ N(0, σ2I), show that the least-squares solutionβ^solving the normal equations ATAβ� � = ATy is the maximum likelihood estimator for β�.
6. For a linear regression model.
(a) Determine the joint distribution of the least-squares solution β�^.
(b) Using (a), determine the distribution of the linear regression line at an arbitrary explanatory point x, that is, the distribution of Y^ where Yβ^ = β�0^ + β��^1x.
Comment on how to go about constructing a con�dence interval for the linear regression line at an arbitrary explanatory point x.