Response te following:
Questions
Assume that there are three assets available. A is a risk-free asset with that yields a rate of 8%. The other two assets, B and S are risky asset with the following attributes.
Asset Expected Return Standard deviation
A
B 12% 15%
S 20% 30%
Correlation between assets B and S is 0.1.
Question 1:
To determine the investment proportions in the minimum-variance portfolio of the two risky assets, the expected value and standard deviation of its rate of return. I did the following : {see attachment}
Question 2:
To draw the investment opportunity set of the two risky funds. I used investment proportions for the stock funds of zero to 100% in increments of 20%.
Tabulate the investment opportunity set of the two risky funds {see attachment}
|
Investment Proportion of Stock Fund
|
Investment Proportion of Bond Fund
|
Portfolio Standard Deviation
|
Portfolio Expected Return
|
|
0.00%
|
100.00%
|
15.00%
|
12.00%
|
|
20.00%
|
80.00%
|
13.94%
|
13.60%
|
|
40.00%
|
60.00%
|
15.70%
|
15.20%
|
|
60.00%
|
40.00%
|
19.53%
|
16.80%
|
|
80.00%
|
20.00%
|
24.48%
|
18.40%
|
|
100.00%
|
0.00%
|
30.00%
|
20.00%
|
Draw the investment opportunity set of the two risky funds
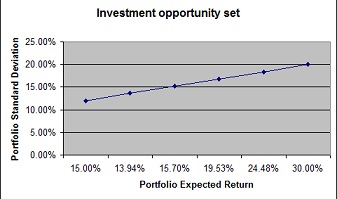
Question 3:
If using only risky assets S, and B, to set up portfolio to yield an expected return of 14%, I did the following {see attachment}
|
Investment Proportion of Stock Fund
|
Investment Proportion of Bond Fund
|
Portfolio Standard Deviation
|
Portfolio Expected Return
|
|
25.00%
|
75.00%
|
14.13%
|
14.00%
|
Question 4:
Using all three assets A, B, and S, how can I set up portfolio to yield an expected return of 14%? What would be the standard deviation this portfolio? What proportion of each asset invested?
Question 5:
Assuming the borrowing is not allow, to construct a portfolio of only risky assets S, and B, with an expected return of 24%. What would be appropriated portfolio proportions? Consequently, what are their standard deviations? If the borrowing is allowed at the risk free rate, how much less the standard deviation would be?