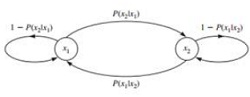
Solve the following problem:
A first-order Markov source is characterized by the state probabilities P(xi),i =1, 2,..., L, and the transition probabilities P(xk |xi), k = 1, 2,..., L, and k ≠ i. The entropy of the Markov source is
L
H(X) = Σ P(xk)H(X |xk)
k=1
where H(X|xk ) is the entropy conditioned on the source being in state xk. Determine the entropy of the binary, first-order Markov source shown in Figure, which has the transition probabilities P(x2|x1) = 0.2 and P(x1|x2) = 0.3.
Note that the conditional entropies H(X|x1) and H(X|x2) are given by the binary entropy functions Hb(P(x2|x1)) and Hb(P(x1|x2)), respectively. How does the entropy of the Markov source compare with the entropy of a binary DMS with the same output letter probabilities P(x1) and P(x2)?