Determine the cartesian equation of the plane that has x-

Question

Part -1:

1. Is the line containing the line segment ^→PQ perpendicular to the line containing the line segment ^→QR?

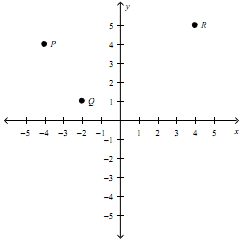
2. Determine the Cartesian and vector equations of the line shown below.

3. Determine two sets of parametric equations for the line passing through the points P( 1,7, 1) and Q ( 3, 4, 4).

4. Determine the x-, y-, and z-intercepts of the plane with vector equation r^→ = (-1, 2, 3) + s (-2, 2, 3) + t (-3, 2, 6), s, t ∈ R.

5. Is there a plane that is perpendicular to the plane 2x - 3z + 4 = 0 containing the point P( 2, 3,-7)?

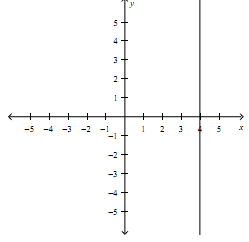
6. Determine the equation corresponding to the following sketch.

Problem Solving

7. Let L 1 be the line r' = ( 2, 9) + s (1, 1), s ∈ R. Let L2 be the line v = (-3, 2) + t( 1, 2), t ∈ R. Find the intersection of these two lines, and then find the area of the triangle whose vertices are the intersection point, s= 0 on L₁, and t= 3 on L₂.

8. a. Show that two lines with direction vectors d₁^->, = ( 2, 3) and d₂^-> = ( 6,-4) are perpendicular.

b. Give the Cartesian equation of the line with direction vector d₁ going through the point P(5,-2) .

c. Give the vector equation of the line from part b.

9. a. Determine the vector and parametric equations of the plane that passes through the points Q(-3/2, 0, 0),  R(0. -1.0) , and S( 0, 0, 3).

b. Determine if the point P( 1, 5, 6) is a point on this plane.

10. a. Determine the Cartesian equation of the plane that has x-, y-, and z-intercepts at 2, -4, and 3 respectively.

b. Determine the Cartesian equation of the plane that passes through the origin and is parallel to the plane in part a.

c. Determine the vector equation of the line of intersection of the plane in part b. and the xy-plane.

Part -2:

1. L₁: (7, 21,-3 + s(0, 3, -2), s ∈ R and L₂: ( 1 1, - 1, 6) t (-4, 4, 3), t ∈ R intersect at point A. Determine the vector equation for the line that passes through point A and the origin.

 

2. If two planes intersect at a line with direction vector m = (-14, 52, 17) and one plane is given by the equation x - 3y + 10z = 24, determine a possible normal vector for the second plane?

 

3. Show that the following system has no solutions.

x-y+ 9z = 10

-4x+y-z =0

-2x+ 2y- 18z = -2

 

4. Calculate the distance between the lines x - 3y= 1 and x- 3y= 10.

 

5. Use the distance formula to determine the distance between the point ( 2, 1, 6) and the yz-plane.

 

6. In how many different ways can you describe a single line?

 

7. Show that the line of intersection between the planes 2x + y - 3z = 7 and -x + 4y + z = 2 lies on the plane 3x - 3y - 4z = 5.

 

8. Explain why the following system has no solution.

 

5x- 3y-z= 6

 

2x+y-7z= -10

 

1       7      3

 

x+ 2y- 2z= 2

 

9. Determine the coordinates of the point that is a reflection of the point (3, 2 about the line -4x + 3y + 2 = 0.

 

10.  Two lines have equations L ( 0, 0, 1) + s(1, -1, 1), s ∈ R and L₂: (2, 1, 3) + t(2, 1, 0), t ∈ R . What is the minimal distance between the two lines?