Assignment:
Problems:
1. Three point charges q1 = +6.0 μC, q2 = -3.0 μC, and q3 = -3.0 μC are placed on the corners of an 4.0 cm (height) by 3.0 cm (width) rectangle as shown in the figure to the right.
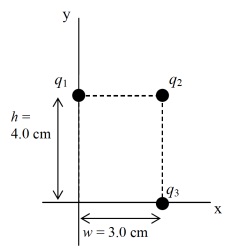
a) Find the net force (in vector form) on q2: F→2net
b) Find the electric field, E→, in vector form at the origin, (0,0), for the given configuration of all three charges shown.
The same setup of three point charges q1 = +6.0 μC, q2 = -3.0 μC, and q3 = -3.0 μC is used for parts (c) and (d) below. It is reproduced here so you don't have to page back and forth to the prior page.
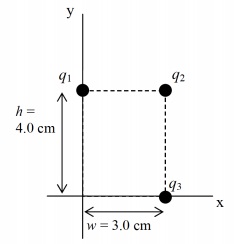
c) Find the electric potential, V, at the origin, (0,0), for the given configuration of all three charges shown. (You may assume that the electric potential is equal to zero at infinity, i.e. V(∞)= 0.
d) Find the magnitude (only) of the force that an electron would feel if placed at the origin. Hint: you may use the results of any of the prior calculations that you deem useful!
2. A sphere of radius R is surrounded by a concentric spherical shell of inner radius 2R and outer radius 3R, as shown to the right. The inner sphere is an insulator containing a net charge +Q distributed uniformly throughout its volume. The spherical shell is a conductor containing a net charge +5Q.
Use Gauss's law to determine the electric field for the following values of r, the distance from the center of the insulator. Clearly show all work for full credit.
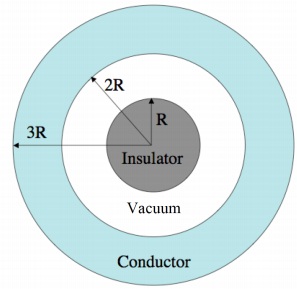
a) 0 < r < R (inside the charged insulator).
b) R < r < 2R (in the vacuum between the insulated and conducting sphere).
c) 2R < r < 3R (in the conducting sphere).
d) 3R < r (outside both spheres).
Determine the surface charge density a (charge per unit area) on e) the inside surface of the conducting shell;
g) Determine the potential V(3R) at the outside surface of the conducting shell relative to the potential at infinity, which is set equal to zero, i.e. V(∞)0.
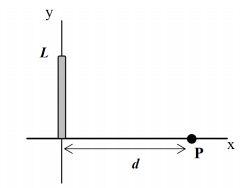
3. Electric charge Q is distributed uniformly along a line (or thin rod) of length L. Find the electric potential at point any P located some distance, d, along the x-axis, as shown in the figure to the right.
4. Two identical parallel plate capacitors, each with capacitance C1= C2 = 4.00 uF, are connected in series with a 10.0 Volt battery, as shown to the right. The plates are separated by a 5.00 mm distance.
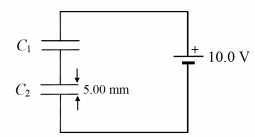
a) Calculate the equivalent capacitance.
b) What is the total charge residing on each plate?
c) What is the electric field (direction and magnitude) between the plates of each capacitor?
Without changing anything else (the battery also remains connected), we fill the entire air gap of the top capacitor with a dielectric (K = 3).
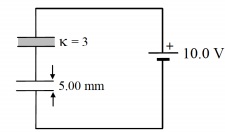
d) What now is the total charge residing on each plate?
e) What now is the electric field (direction and magnitude) between the plates of each capacitor?
f) Calculate the total energy stored in this capacitor network, i.e. the one shown above with the dielectric inserted in the top capacitor.
g) Did the energy stored in the capacitor network increase, decrease, or stay the same when the dielectric was inserted? Briefly justify your answer.