Assignment:
Bernoulli's equation determines ejection velocity of liquid from a tank. Motion equations find x,y coordinates of impact of the liquid.
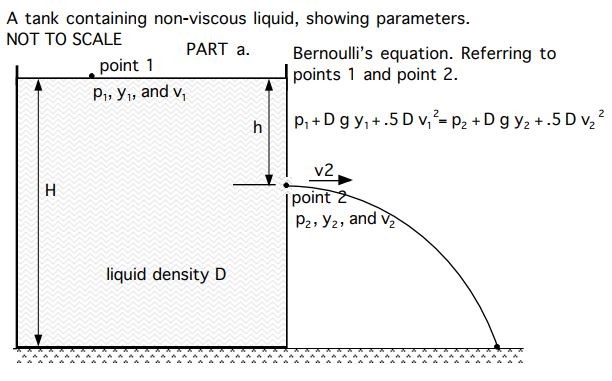
A large tank contains non-viscous liquid whose depth is H. A bullet punches a small hole of radius r in the vertical side of the tank at a point which is distance h below the liquid surface.
See diagram showing parameters and Bernoulli's equation.
a. Apply Bernoulli's equation to determine distance h such that the emerging liquid impacts the ground at maximum distance from the base of the tank which is resting on the ground. Give the answer as h in terms of H.
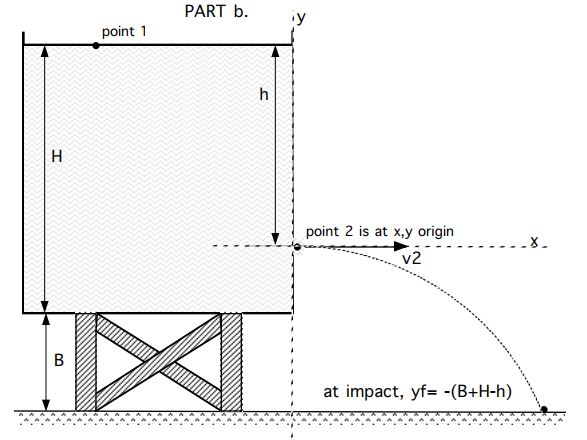
b. The same tank, containing the same liquid at depth H= 8 m, is now placed on a support so that its bottom surface is distance B= 15 m above the ground. The hole of radius r= .03 m is made at a point which is at a depth h=6 m below the lliquid surface. For an x,y origin at the hole, find the x coordinate of the impact point.
c. For knowns as quoted in PART b, find the volume of liquid which emerges from the hole in the first 18 seconds. (Assume the total depth of the liquid remains unchanged.)