Determine a generic function

Question

Assignment:

For a generic function g(n) defined for n ≥ 0, we define its z-transform as

Z(g)(z)= ^∞Σ_n=0 g(n)zⁿ

where z is a complex variable. With reference to the bidirectional random walk of Example 7.2 M develop the following points.

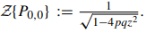
a) Prove that

b) Using the result of the previous point, derive the exact expression of

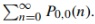
c) Prove that Z{ƒ0,0}= 1 - √1-4pqz².

d) Using the result of the previous point, derive the exact expression of f0,0 and of f0,0(n) for any positive integer n.