Determine the coefficient of thermal expansion in mmk

Question

The potential energy between two atoms can be represented as follows:

V = - A/r + B/r¹⁰

Where A and B are constants and r the interatomic separation distance. Plot the potential energy verses distance relationships for these atoms when A= 5 x 10^-30 J.m and B= 8 x 10^-121 J.m¹⁰. Determine the coefficient of thermal expansion (in m/m.K) for the material over the following temperature ranges:

a) 0^oK to 0^oC,

b) 0^oC to 820^oC.

assume that thermal energy of the system is 3kT/2 where k is Boltzman's constant k = 1.381 x10-23 J/K.

2. Calculate the density of BaTiO₃. It has the perovskite structure. In the perovskite structure, the Ba²⁺ and O^2-combine to form a cubic close packed structure with the Ba²⁺ on the cube corners and the O^2- in the face centre positions (because the Ba²⁺ and O^2- have nearly the same radius). The small Ti⁴⁺ fits nicely in an octahedral site. Because of stoichometry and charge neutrality, only ¼ of the octahedral sites (those in the body centre position) are filled with Ti⁴⁺. See figure below.

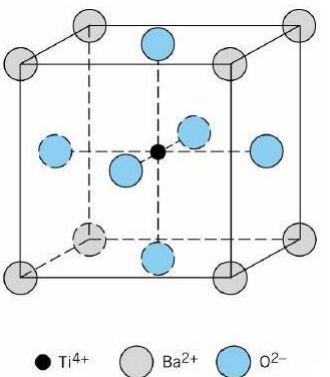
Ionic Radius                     Atomic Mass
Ba²⁺ 1.36 Ångstroms        137.3 g/mole
Ti ⁴⁺ 0.61 Ångstroms         47.9 g/mole
O^2- 1.40 Ångstroms           16.0 g/mole

Avogadro's number (NAv) is 6.02 x 10²³ atoms per mole.

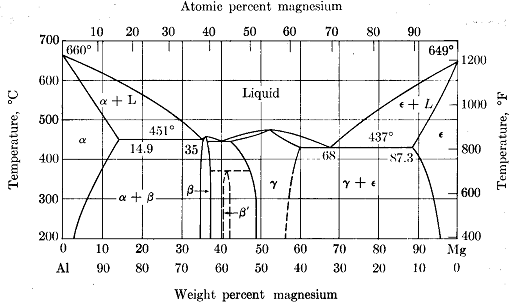
3. Using the phase diagram below for the aluminium-magnesium system, determine

i. the phases present and
ii. the composition (wt% Mg) of each phase and
iii. the amount of each phase for:

a) an aluminium-magnesium (5 wt % Mg) alloy at 500 ^oC.
b) an aluminium-magnesium (20 wt % Mg) alloy at 550 ^oC.
c) an aluminium-magnesium (80 wt % Mg) alloy at 300 ^oC.