Assignment:
Two or three players are about to play a game: with probability 1/2 the game involves Players 1 and 2 and with probability 1/2 the game involves Players 1, 2, and 3. Players 2 and 3 know which game is being played. In contrast, Player 1, who participates in the game under all conditions, does not know whether he is playing against Player 2 alone, or against both Players 2 and 3. If the game involves Players 1 and 2 the game is given by the following matrix, where Player 1 chooses the row, and Player 2 chooses the column:
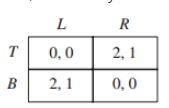
with Player 3 receiving no payoff. If the game involves all three players, the game is given by the following two matrices, where Player 1 chooses the row, Player 2 chooses the column, and Player 3 chooses the matrix:
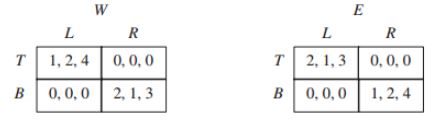
(a) What are the states of nature in this game?
(b) How many pure strategies does each player have in this game?
(c) Depict this game as a game with incomplete information.
(d) Describe the game in extensive form.
(e) Find two Bayesian equilibria in pure strategies.
(f) Find an additional Bayesian equilibrium by identifying a strategy vector in which all the players of all types are indifferent between their two possible actions.
Provide complete and step by step solution for the question and show calculations and use formulas.