Answer all the questions.
Q.1 Maximise z = 3x1 + 4x2
Subject to constrains 5x1 + 4x2<= 200;
3x1 + 5x2<= 150;
5x1 + 4x2<= 100;
8x1 + 4x2>= 80,
x1>= 0, x2>= 0
Q.2 State the ways in which customers in a queue are served.
Q.3 Describe the use of simulation in networks? What are the advantages of using simulation?
Q.4 Describe maximin-minimax principle. Briefly explain the characteristics of competitive game
Q.5 A project has 10 activities. The following table shows the information about the activities.
Table 14.5: Activities information
Activity Preceding activity Duration in weeks
A – 6
B – 3
C A 5
D A 4
E A 3
F C 3
G D 5
H B, D, E 5
I H 2
J I, G, F 3
• Draw the network
• Find the project duration
• Identify the CPM
• Prepare the schedule
Q.6 Discuss different types of service systems?
Answer all the questions.
Q.1 Describe project management (PERT) & Project scheduling of PERT.
Q.2 Write down a short note on Monte-Carlo simulation? What are the Limitations of using Simulation?
Q.3 In a rectangular game, pay-off matrix of player A is as follows:
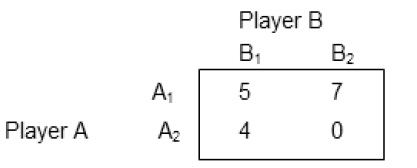
i) Solve the game.
ii) Write down the pay-off matrix of B and then, solve the game.
Q.4 A marketing manager has 5 salesmen and 5 sales districts. Considering the capabilities of the salesman and the nature of districts, the marketing manager estimates that the sales per month (in hundred rupees) for each salesman in each district will be as follows.
Sales districts
A B C D E
1 32 38 40 28 40
2 40 24 28 21 36
3 41 27 33 30 37
4 22 38 41 36 36
5 29 33 40 35 39
Find the assignment of salesman to districts that will result in maximum sales.
Q.5 Describe PERT & CPM. Write down the essential difference between PERT and CPM.
Q.6 Describe Linear programming problem by giving two examples & write any 3 applications of Linear Programming problem.