Describe the driving frequency curve for driven oscillator

Question

Assignment:

Problem 1.

A) List two effects that increasing the damping on a driven harmonic oscillator would have on the average-power-delivered vs driving frequency curve?

B) In steady state, does a driven oscillator oscillate at the frequency of the driving force, the natural frequency of the oscillator or neither of these frequencies?

Problem 2.

A driven oscillator has a resonant frequency of 100 rad/s and a damping rate of 20/s. When the frequency of the harmonic driving force is 100 rad/s the average power delivered to the oscillator is 10 W. What will be the average power delivered to the oscillator when the frequency of the driving force is

A) 90 rad/s?

B) 110 rad/s?

C) 10 rad/s?

D) 400 rad/s?

Problem 3. Sketch by hand the average power vs driving frequency curve for the driven oscillator described in Problem 2.

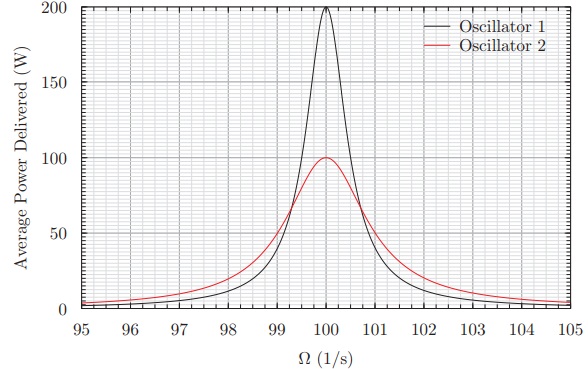
Problem 4. Consider two identical blocks attached to two dierent springs each of spring constant 200 N/m. The masses can move along the x-direction. Both masses are driven by identical external forces (with an x-component) given by F_driving;x = F₀ cos(Ωt)

Here, t is time and Ω is the variable driving frequency. The average powers delivered to the oscillators vs driving frequency curves are plotted below. Using the plot and the given information determine

A) the mass of the blocks.

B) the damping rate r for each oscillator.

C) The quality factor Q for each oscillator.

D) The damping parameter b for each oscillator.

E) The amplitude F₀ of the driving

Problem 5. Repeat the steps leading from Equation 5 to Equations 9 and 10. Fill in missing steps as you do so.

Problem 6. Which of the following functions represent nondispersive waves? For each nondispersive wave form indicate the speed and direction of wave motion and the direction that the medium would move. Assume that x; y; and z are coordinates, t is time, and all other symbols are positive constants.

A) y = A sin(k (x + vt) + π )

B) z = A cos(k (y² ¡ gt))

C) z = A cos(k (y ¡ gt))

D) y = A e^{-(5/m)(x-(10m/s)t)2} cos((5/m)(x - (10 m/s)t))

E) y = A e^{-(5/m)(x-(10m/s)t)} cos((5/m)(x - (7 m/s)t))

F) x = A e^-h(at+z)2 cos(r (a t + z))

G) y = A (x + vt) cos(k (x + vt))

H) z = A (x² + vt²)

Problem 7. Consider the waveform

z = (1.5 m)sin [(10π/m)x +(2π /s)t]

A) Find the wavelength.

B) Find the frequency in rad/s.

C) Find the frequency in Hz.

D) Find the speed of the wave and the direction of propagation of the wave.

E) Along what direction do points in the medium move?

Problem 8.

A) Write a function that describes the motion of a string as a wave traveling in the ¡z direction with speed 200 m/s and frequency 40 Hz passes through the string. Assume that the wave is a transverse wave and that the medium moves back and forth along the x -direction. Let the amplitude of the motion be 2 m. Make sure that you include units at all of the appropriate places in your function.

B) Repeat part A) if the same string is used but the frequency is changed to 10 Hz.

Problem 9. One end of a spring is shaken up and down at a rate of 10 times per second. The resulting harmonic wave is measured to have a wavelength of 1 m and an amplitude of 0.5 m. Let the direction of wave propagation be the negative x direction and let the spring particles move up and down along the z direction.

A) Write down a waveform that describes the wave in this spring.

B) Write down a waveform that describes the wave that would result in this spring if the shaking rate is changed to 2.5 times per second.