Question 1)a) Derive the Navier Stokes Equation in its non conservative form using a suitable model of flow.
b) With an example explain the phenomenon of divergence of velocity field
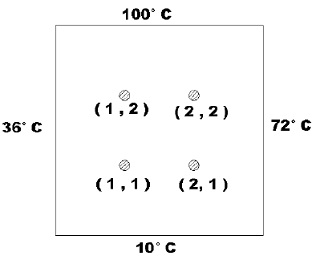
Question 2) Using Gauss Seidel method with SOR solve for the temperature distribution in a plate whose edges are maintained at specified temperature (as in figure below).Consider the weight factor = 1.5. Also mention the error at each node after 3rd iteration
Question 3) With a neat flow diagram explain the SIMPLE algorithm of Patankar-Spalding
Question 4)a) Explain what is the meaning of the Conservative and Non-conservative forms of the flow equations.
b) With neat sketches, explain the following boundary conditions. (i)Outlet (ii) Constant pressure
Question 5)a) With an example explain false diffusion?
b) Derive the steady one dimensional convection diffusion equation in discretized form.
Question 6)a) Brine solution of Specific Gravity of 0.9 is flowing in a square duct of side 25 mm. It enters the duct with a temperature of 60°C. The velocity of flow is assumed to remain constant at 8 m/s. The diffusive flux (Γ) through the duct can also be assumed to be constant at 800 kg/m/s. The length of the duct is 900 mm. Exit temperature of the solution is 20°C. Apply the following discretization schemes and obtain the temperature distribution along the duct. (1) Central Difference Scheme (CDS) (2) Upwind Differencing Scheme (UDS).Use three equally spaced grids to descritize the domain.