Assignment:
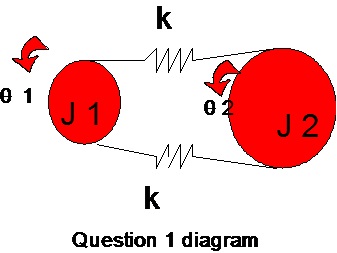
Question 1. A pulley 250mm in diameter drives a second pulley 1000mm diameter by means of a belt.The mass moment of inertia of the drive pulley is 0.2kg-m2. The belt connecting these pulleys is represented by two springs, each of stiffness k. Find a value for k for which the natural frequency is 6 Hz. Derive the equation of motion for this system.
Question 2. A DVD drive is mounted on a chasis and is modelled as a single degree of freedom spring, mass and dampener. During normal operation, the drive (having a mass of 0.4kg) is subject to harmonic force of 1N at 10 Radians per second. Because of material considerations and static deflection, the stiffness is fixed at 500N/m and the natural damping in the system is 10kg/s. The DVD player starts and stops during its normal operation providing initial conditions to the module of x0 =0.001m and v0 = 0.5m/s. The DVD drive must not have an amplitude of vibration greater than 0.008m even during transient stage. First compute the response by numerical simulation to see if the constraint is satisfied. If the constraint is not satisfied, find the smallest value of damping that will keep the deflection less than 0.008m
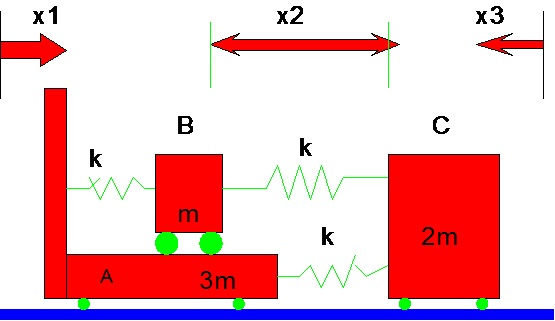
Question 3. A system is made up of three particles interconnected by springs as shown in the drawing. The motion of the system is to be described by the co-ordinates x1, x2 and x3 with x1 and x3 being absolute co-ordinates and x2 being the relative motion between particles B and C. The springs unstretched when x1=x2=x3=0.
(a) Determine the equation of motion of the system in terms of the generalized co-ordinates shown in the drawing and described above.
(b) Find the natural frequencies and mode shapes for the system. Let m = 10kg and k=4000N/m
(c) The system is released with the spring between A and B compressed 0.1 metre and the remaining springs unstretched/uncompressed. In addition, B is given an initial (absolute) velocity of 5m/sec to the right with A and C being at rest. For these initial conditions, find the response of particle C for t > 0. Make a sketch of x3(t).