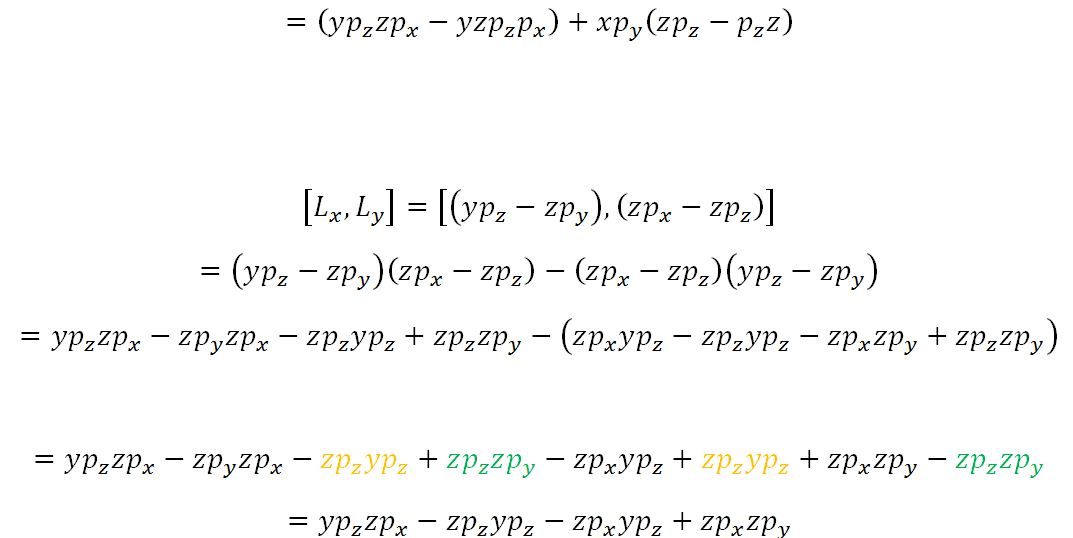Discuss thebelow:
Orbital Angular Momentum
Consider a particle described by the Cartesian coordinates (x, y, z) = x and their conjugate momenta (px, py, Pt) = p . The classical definition of the orbital angular momentum of such a particle about
the origin is L=XXp. giving
L = ypx-zpy, (290)
Ly= z Px - (291)
Lx = xPy - YPx. (292)
Let us assume that the operators (Lx, Ly, Lx) 7Z- L which represent the components of orbital angular momentum in quantum mechanics can be defined in an analogous manner to the corresponding
components of classical angular momentum. In other words. we are going to assume that the above equations specify the angular momentum operators in terms of the position and linear momentum operators. Note that L, . Ly . and LL are Hermitian. so they represent things which can. in principle. be measured. Note. also. that there is no ambiguity regarding the order in which operators appear in products on the right-hand sides of Equations (222)-(2921 because all of the products consist of operators that commute.
The fundamental commutation relations satisfied by the position and linear momentum operators are [see Equations (114)-(116)]
[x1, xi] = 0,
= 0,
[xi, pi] = i h 64,
where i and j stand for either X . y or Z . Consider the commutator of the operators 4 and 4 :
[Lx , Ly] = - Z Pv),(Z - x = + x pyrz, Pz ih(-y x py)= ifiLz.