Defining bounded area formula

Question

Assignment:

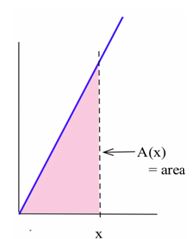
Q1. Define A(x) to be the area bounded by the t-axis, the line y = 2t and a vertical line at t = x.
(a) Find a formula for A(x).
(b) Determine A'(x)

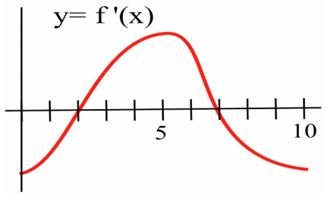
Q2. The figure below shows the graph of the derivative of a continuous function f .
(a) List the critical numbers of f .
(b) What values of x result in a local maximum?
(c) What values of x result in a local minimum?

Q3. Use information from the derivative of each function to help you graph the function. Find all local maximums and minimums of each function.

g(x)=2x³-15x²+6

In 4 and 5, a function and values of x so that f ‘(x) = 0 are given. Use the Second Derivative Test to determine whether each point (x, f (x)) is a local maximum, a local minimum or neither.

Q4. h(x)=x⁴-8x²-2; x=-2,0,2

Q5. f(x)=x·In(x); x=1/e

Q6. Lest you have forgotten, the formulas you will need are as follows:
For a right circular cylinder of radius “r” and height “h”:
The volume V = πr²h.
The surface area S = circular ends plus the cylindrical wall = 2πr² + 2πrh.

You have been asked to design a one-liter (i.e., 1000 cm3) can shaped like a right circular cylinder (figure below). What dimensions will use the least material?

So the question is: What should “r” be and what should “h” be such that the volume is 1 liter but the surface area is least?

Provide complete and step by step solution for the question and show calculations and use formulas.