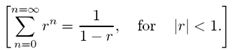Discuss the below:
Q: Define the partition function Z for a system in terms of the energies E1 of its quantum states j and the inverse temperature /3 = (I T)''. Write down the probability pj that the system is in a given state j.
Show that the system's internal energy U, entropy
S = -KB∑jpjlogepj
and Helmholtz free energy F are given by
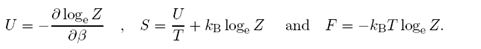
In a simplified model of a crystal, each molecule is a point mass that is attached to its site by a force, so that at each site there is a three-dimensional quantised har¬monic oscillator with natural angular frequency w. Show that in this approximation the Helmholtz free energy of a crystal of N sites is
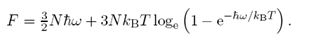
Show that the crystal's heat capacity (a) tends to 3Nk8 in the limit of high temperature, T co, and (b) vanishes in the limit of low temperature, T 0