Define a linear map t from the vector space c to the vector

Question

Problem A.

1. The linear map T : R³ -> R⁴ is given by the matrix

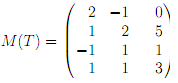
with respect to the standard bases in R³ and in R⁴. Find bases of Ker T and ImT.

2. Let S denote the set of polynomials in R[z] that have degree at most 5 and root 3/2 . Is S a vector space over R? Justify your answer.

In the case of armative answer compute the dimension of S.

3. (a) Show that C = {z = x + y√-1 : x; y ε R} is a vector space of dimension 2 over R.

(b) Define a linear map T from the vector space C to the vector space Mat(2; 2;R) of 2  2 matrices by the rule

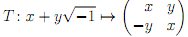
Compute dim ImT.

(c) Show that T(z₁z₂) = T(z₁)T(z₂), where z₁z₂ is a usual multiplication of two complex numbers z₁ and z₂, and T(z₁)T(z₂) is the matrix multiplication of the two corresponding matrices.

4. Suppose linear maps T 2 L(V;W) and S 2 L(W; U) of finite-dimensional vector spaces are given. Show that

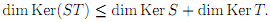
5. Show that the set of invertible n x n matrices (that is, the ones that correspond to invertible linear maps from Fn to Fn) is a group with respect to the matrix multiplication and with the identity matrix I (which has ones along the main diagonal and zeroes otherwise).