Assignment:
Solve these problems are on curvilinear one dimensional systems:
Question 1. Which of the following forces is conservative? (a) F = k (x, 2y, 3z) where k is constant. (b) F = k (y, x,0). (c) F = k (-y, x, 0). For those which are conservative, find the corresponding potential energy U, and verify by direct differentiation that F = - ∫U.
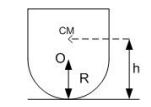
Question 2. The figure shows a child's toy, which has the shape of a cylinder mounted on top of a hemisphere. The radius of the hemisphere is R and the CM of the whole toy is at height h above the floor. (a) Write down the gravitational potential energy when the toy is tipped to an angle � from the vertical.(b) For what values of R and h is the equilibrium � = 0 stable?