Part A: Multiple Choice:
1. The cumulative probability distribution of a random variable X gives the probability that X is _______ to , some spacified value of X.
a. Greater than or equal
b.Equal
c. Less than or equal
d. None of the above
2. What is the probability of P(-1.4 < Z < 0.6)?
a. 0.9254
b. 0.6449
c. 0.3427
d. 0.9788
3. By using the binomial table, if the sample size is 20 and p equals to 0.70, what is the value for P(X18)?
a. 0.0279
b. 0.0375
c. 0.1820
d. 0.1789
4. In a standard normal distribution, what is the area which lies between Z = -1.72 and Z = 2.53?
a. 0.8948
b. 0.9123
c. 0.9516
d. 0.8604
5. What is the value for 95% confidence interval for if = 7.3, x = 84.2, and n = 40.
a. 81.93786.463
b. 68.76772.033
c. 74.09379.337
d. 61.36466.846
6. The __________ is the smallest level of significance at which H0 can be rejected.
a. value of α
b. probability of committing of Type I error
c. p value
d. value of 1- α
7. We say that sample results are significant when _____________________.
a. H0 is not rejected
b. H0 is rejected
c. is smaller than the p value
d. the computed value of the test statistic falls in the acceptance region
8. We commit a Type 1 error if we _________ a true null hypothesis.
a. fail to reject
b. accept
c. reject
d. compute
9. Given:H0: µ = 10, Ha: µ ≠ 10, n = 12, α = 0.01, and the computed test statistic is 2.394, the p value for the test is ____________.
a. between 0.02 and 0.01
b. between 0.025 and 0.01
c. between 0.05 and 0.02
d. none of the above
10. We say that sample results are significant when ___________.
a. H0 is not rejected
b. H0 is rejected
c. is smaller than the p value
d. the computed value of the test statistic falls in the acceptance region
11. You perform a hypothesis test about a population mean on the basis of the following information: n = 50, = 100, α = 0.05, s = 30, Ha: µ < 110. The computed value of the test statistic is ________ .
a. -2.3570
b. -1.645
c. 2.3570
d. 4.24264
12. Given: H0: µ ≥ 100, the alternative hypothesis is _________ if the test is one-sided and the critical value is negative.
a. µ < 100
b. µ > 100
c. µ = 100
d. µ ≠220
13. You perform a hypothesis test about a population mean on the basis of the following information: The sampled population is normally distributed with a variance of 100, n= 25, = 225, α = 0.05, Ha: µ > 220. The critical value of the test statistic is ______
a. 2.5
b. 1.645
c. 1.7109
d. 1.96
Part B: Fill in the blank:
14. The purpose of hypothesis testing is to aid the manager or researcher in reaching a (an) __________ concerning a (an) _____ by examining the data contained in a (an) _________ from that ___________.
15. A hypothesis may be defined simply as _______________.
16. There are two statistical hypotheses. They are the ___________ hypothesis and the ___________ hypothesis.
17. A Type I error occurs when the investigator ______________.
18. Values of the test statistic that separate the acceptance region from the rejection are called ___________ values.
19. The probability of obtaining a value of the test statistic as extreme as or more extreme than that actually obtained, given that the tested null hypothesis is true, is called __________ for the _________test.
20. When one is testing H0: µ= µ0 on the basis of data from a sample of size n from a normally distributed population with a known variance of σ2, the test statistic is __________.
21. The null hypothesis contains a statement of ______________.
22. The statement µ ≥ 0 is an inappropriate statement for the __________ hypothesis.
23. The null hypothesis and the alternative hypothesis are _________ of each other.
24. Please consider “reject” or “fail to reject” by using one tailed and two-tailed method (Part A&B):
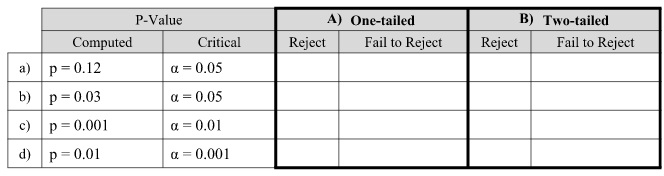
Part C: Answer the following questions:
25. Explain the differences between discrete random variable and continuous random variable.
26. What are the characteristics of discrete probability distribution?
27. When should the z-test be used and when should t-test be used?
28. Explain the following concept:
a) Central Limit Theorem
b) Type I error and Type II error
Part D: Must show all your work step by step
29. The random variable X has a normal distribution with mean 50 and variance 9. Find the value of X, call it :
30. Use the below information to fill in the table and answer the following questions.
x P(X=x)
0 0.112
1 0,238
2 0.014
3 0.234
4 0.071
5 0.069
6 0.114
7 0.148
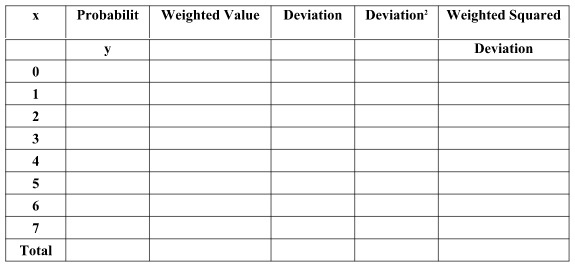
Please answer
a) Mean b) Variance c) Standard deviation
31. Determine the following probabilities by use of the table of binomial probabilities.
A. P(X=1 | n=10, p=0.40)
B. P(X=2 | n=10, p=0.70)
C. P(X≤16 | n=50, p=0.50)
D. P(X<5 | n=10, p=0.60)
E. P(X≥8 | n=50, p=0.80)
32. Twenty trails are conducted in a Bernoulli process in which the probability of success in a given trail is 0.6. If x = the number of successes determine the following:
a. E(X)
b. σx
c. P(X=4)
d. P(2≤x≤6)
e. P(x>5)
33. Use the following information to conduct the confidence intervals specified to estimate μ.
a. 95% confidence; =25, = 12.25, and n=60.
b. 98% confidence; =119.6, = 570.7321, and n=25.