Tracings on the Ice
Below are two projections of the skate blade tracings that are created during KeaunaMacLaughlin and Rockne Brubaker's death spiral.
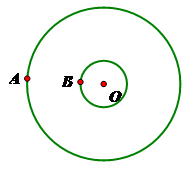
The projection on the left, depicting concentric circles, is a bird's eye view of the tracings that Keauna and Rockne form when completing the death spiral. In both projections, Rockne's center of mass is at point O. The circle representing Keauna's blade trajectory has radius, OA. The circle representing Rockne's blade trajectory has radius, OB.
Answer the following questions about the death spiral:
• Does Keauna or Rockne travel faster during the death spiral? Explain how you determined your answer.
• If OA = 10 feet, and OB = 2 feet, answer the following questions:
o How much further does Keauna travel than Rockne? Explain.
o If the death spiral took 8 seconds to complete, what is the difference in speeds of Keauna and Rockne? Explain.
o Keauna and Rockne's friend, Lisa, is trying to answer previous two questions and she first calculates the difference between the lengths of OA and OB. Is this a valid first step to solve the above two questions? If so, how could she use it, and if not, explain why not.
o If Rockne's rate is 1.05 feet per second, then how much time did the death spiral take? What is Keauna's speed during the death spiral? Explain.
• Keauna and Rockne completed a death spiral that lasted 4 seconds. Keauna's rate was 12.56 feet per second. What is the length of OA? Explain.
Create an activity (e.g., a worksheet, a computer program, etc) that uses mathematical modeling of another context. Identify the Common Core State Standards content standards that your activity addresses. Provide solutions for your activity.