Discuss the following problem:
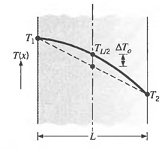
Q: Measurements show that steady-state conduction through a plane wall without heat generation produced a convex temperature distribution such that the mid- point temperature was 6.To higher than expected for a linear temperature distribution.
Assuming that the thermal conductivity has a linear dependence on temperature, k = ko (1 + aT), where a is a constant, develop a relationship to evaluate a in terms of ΔT0' T1, and T2.