Problem 1. Speaking in Real Terms: CPI and Nominal Values Adjustment.
The following table shows information about the CPI - U between 1989 and 2014. This index is similar to the standard CPI but includes the all - urban consumer population and excludes rural consumers, the military and institutional population. You can download the historical series from 1913 in https://www.bls.gov/cpi/tables.htm (detailed reports).
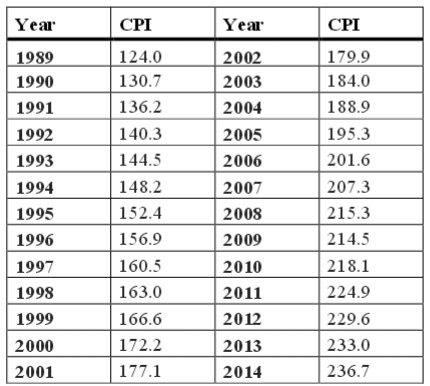
a. You can think of the CPI - U index as a more accurate measure of inflation if you want to compare the cost of living in urban areas. Using the information above, compute the annual inflation rate in the US economy. Put your answers in a table with the following format (notice you will need to expand the table to include all the years from 1990 through 2014).
b. Now, compute the inflation rate between 1990 and 2000 and then between 2000 and 2010 (inflation rate measured over a decade or ten - year period of time). Put your answers in the following table:
c. Assume that the salary for a professor was $90,000 in 1991, $140,000 in 1998 and $200,000 in 2012. Convert all of these salary amounts from current dollar measures to constant dollars where the base year is 2014 (so convert to 2014 dollars). In what year did the professor earn more in real terms?
d. Suppose that on January 1, 1995 a bank lends $10,000 to a person. The bank and the individual both agree that the real interest rate charged on the loan should be 10% and the loan is going to be totally paid ($10,000 plus interest), in a one - time payment, on December 31, 1996. Suppose the two parties to this transaction can perfectly foresee what the inflation rate for this period is going to be. Given this information, what is the nominal rate the Bank has to charge on this loan? Assume that the CPI is computed at the beginning of each year.
e. Assume the same conditions exist as in question 1d, but now the bank and the borrower cannot predict the inflation rate perfectly. Assume that both the bank and the borrower expect an inflation rate of 7% over this period of time. Given this information, what is the nominal rate charged on the loan now? Given the actual inflation rate (from your calculations and the provided data), who wins from this loan contract and who loses from this loan contract? Explain your answer fully. What if the expected in flation rate is 3% during this period? Does your answer change as to who wins and who loses? And, if so, why did your answer change?
f. Suppose that in December, 2008 the labor union of a firm is negotiating with the owners of the firm the new nominal wages that are going to prevail during 2009 in the company. Assume the labor union has a perfect forecast of inflation during the relevant period, that is, the expected inflation rate is equal to the actual rate of inflation. Workers know that because of the recession it is difficult to increase real wages for next period and so they agree with the owners of the firm in keeping the real wage constant. Given this information and the data you were provided, by how much should the nominal wage change? Show how you calculated your answer.
g. What if the labor union anticipates that the expected inflation rate is 1% during this period? If the union successfully negotiates a 1% increase in nominal wages for this period, who is better off once the actual inflation rate is accounted for? Explain your answer.
Problem 2. Two Different Aggregate Production Functions. Consider two countries: A and B. The aggregate production function of country A is given by: Y = TK1/2 L1/2
And the aggregate production function of country B is given by:
Y = TKL
where Y is real GDP, T represents the state of the technology, K is units of capital, L is units of labor (in this case, the number of workers). Labor and capital are the only inputs used in both countries to produce real GDP. Initially K is equal to 10 units in both countries. In country A, the state of the technology is represented by T=300 and in country B the technology is T=10. Answer the following questions based on the above information and the table below (you will need to expand it from the truncated form provided here and fill in the missing values using a spreadsheet program). You do not need to submit these tables with your homework, but you do need to submit the graphs drawn from these tables. The graphs need to be generated by the spreadsheet program and NOT hand drawn graphs of the data.
a. Use Excel to graph the relationship between L and Y in country A and country B. Measure L on the horizontal axis and Y on the vertical axis. You will likely find it easier to graph this relationship in two different graphs. Make sure you use a spreadsheet program to draw these graphs from the data you calculated in the above table!
b. Use Excel to draw two graphs that depict the relationship between MPL and Labor Productivity and L. In the first graph represent country A; and in the second graph represent country B (make sure label these graphs completely and carefully). In each graph measure L on the horizontal axis and MPL and Labor Productivity on the vertical axis. For both graphs use Excel, the values you obtained in your spreadsheet program, and the graphing tool to generate these graphs.
c. Describe verbally what happens to the marginal product of labor as the level of labor usage increases in both countries. Does the marginal product of labor show different patterns in the two countries? Which pattern do you think is the one you are more likely to find in the real world?
d. As the amount of labor increases, what happens to labor productivity in each of these countries? Explain why labor productivity exhibits different patterns in country A and country B.
e. Given the information above, complete the following table: assume that L = 40 for both countries. Note: you have already computed these values in the first part of this problem: you just need to complete the table and then discuss this next question in your answer. Which country has a higher GDP, MPL and labor productivity at this point?
L Y MPL Y/L
Country A
Country B
f. Compute the rate of growth of GDP and labor productivity for each country if both of them increase the number of workers from L = 40 to L = 41. Which country has higher rate of growth? Explain your results verbally. You will find it handy to complete the following table before explaining your results. Carry your answer out to two places past the decimal.
g. Now assume that in one decade the capital stock increases in country A by a factor of 4 - so now the capital stock in country A is K = 40. Using your spreadsheet skills draw a new graph of the original aggregate production function for country A when K = 10 and the new aggregate production function for country A when K = 40. Your graph should measure L along the horizontal axis and real GDP along the vertical axis. Make sure this graph is carefully and completely labeled. Then, in your own words, explain the effect on country A's MPL and labor productivity from this increase in capital assuming that country A has L = 40. Fill in the following table to guide your explanation:

h. Suppose that during the same decade, a migration wave arrived in country B and this migration resulted in the number of workers in country B increasing to L = 60. There was no change in the capital stock in country B. Given this information, what happens to real GDP in country B due to this migration wave? Illustrate your answer with a graph of country B's aggregate production function with real GDP measured on the vertical axis and labor measured on the horizontal axis. Label the initial point of production (when L = 40) and the new point of production after the migration wave (when L = 60). Then explain what happens to MPL and labor productivity due to this migration wave. Here's a table to help you organize your answer to this last question.
i. Suppose that country A is producing with L = 40 and K = 40 while country B is producing with L = 60 and K = 10. Furthermore, suppose that country B's GDP increases by 3% per year (we have no idea how they are managing this, we are just accepting this constant annual growth rate). Given these assumptions how many years would it take for country B to reach the GDP level of country A? For this question assume that the GDP level of country A does not change over time: that is, GDP in country A stays at that level associated with L = 40 and K = 40
j. Assume we have the exact same set - up as in part (i) of this question. What would have to be the rate of growth in GDP in country B if country B wants to reach the level of GDP that country A has in 10 years?
Problem 3. Long Run Growth Policies In this exercise we will continue referring to country A from the previous problem. Now assume that the production function is given by: Y = TK1/2 ( HL)1/2 Where, as before, Y is real GDP, T represents the technology, K is units of capital, and L is units of labor. However, there is one difference with respect to problem 2: Now, the production function includes H, a term that captures the level of human capital of the country. You can view this variable as a factor that adjusts for the quality of the labor force: for example, as H increases this means that HL is a larger number and therefore has a larger impact on the final value of Y. Assume T=300, L=40, K= 10 and H=1 as in the initial situation from the previous problem.
a. For this question, draw a graph illustrating the initial aggregate production function and the new aggregate production function if T increases from 300 to 450. Label your graph carefully and completely. The y - axis should measure real GDP and the x - axis should measure labor. Indicate where the economy is producing on each graph given the above information. Then, compute the rate of growth of GDP and the value of GDP per capita (assume that the population is equal to the number of workers country A has). Finally provide an explanation for each of the results you give. You will find it helpful to complete the following table before you write your explanation. Don't forget to draw the graph!
T Y Y/L Growth rate Growth rate of GDP
of GDP (%) per capita (%)
300
450
b. For this question, draw a graph illustrating the initial aggregate production function and the new aggregate production function if human capital increases from H = 1 to H = 1.5. Label your graph carefully and completely. The y - axis should measure real GDP and the x - axis should measure labor. Indicate where the economy is producing on each graph given the above information. Then, compute the rate of growth of GDP and the value of GDP per capita (assume that the population is equal to the number of workers country A has). Finally provide an explanation for each of the results you give. You will find it helpful to complete the following table before you write your explanation. Don't forget to draw the graph!
H Y Y/L Growth rate Growth rate of GDP
of GDP (%) per capita (%)
1
1.5
c. For this question, draw a graph illustrating the initial aggregate production function and the new aggregate production function if the capital stock increases from K = 10 to K = 15 and simultaneously the unit of labor hired (and, by assumption, the population in this problem increases to L = 60. Label your graph carefully and completely. The y - axis should measure real GDP and the x - axis should measure labor. Indicate where the economy is producing on each graph given the above information. Then, compute the rate of growth of GDP and the value of GDP per capita (assume that the population is equal to the number of workers country A has). Finally provide an explanation for each of the results you give. You will find it helpful to complete the following table before you write your explanation. Don't forget to draw the graph!
L K Y Y/L Growth rate Growth rate of GDP
of GDP (%) per capita (%)
40 10
60 15
d. Given this analysis, what policies would you suggest to governments in order to increase the welfare of the population where welfare is measured as GDP per capita? Mention at least one policy per example you worked with in the first three parts of this problem.
Problem 4. Two Faces of the Same Coin: Saving and Investment. Assume the following information about an economy (in million of dollars):
GDP = $1000
C = $800
G = $120
I = $100
X - IM = - $20
T = $80
TR = $10
Where C is private consumption spending, G is public spending, I is investment spending, T represents taxes and TR represents transfers from government to households. Finally, X - IM represents net exports.
a. Given the above information, compute the level of private savings (Sp), public savings (Sg) and net capital inflows (KI). Is the sum of private savings, public savings and net capital inflows equal to the level of investment? What is the value of national savings (SN )?
b. Now, let's change the problem. First, assume that net capital inflows is 0. Now, suppose that Consumption (C) is given by the following equation instead of being a provided value:
C= 380 – 800i.
And, finally suppose that investment is given by the following equation instead of being a provided value:
I = 2500 - 200i, where i is the nominal interest rate.
Given this information and these equations, write an equation for national savings (SN). This equation will contain two variables: SN and i. You will need to use the identities (the underlying relationships) that you used in (a). Show your work and any equations or identities that you use.
c. The Savings Curve represents the supply of funds that are available in the loanable funds market while the Investment Curve represents the demand for funds from the loanable funds market. Given this information and the national savings equation you found in (b) as well as the investment equation you were provided in (b) to calculate the equilibrium interest rate and the equilibrium quantity of loanable funds. That is, find the interest rate and loanable funds that make the supply of loanable funds (i.e, national savings) equal to the demand for loanable funds (i.e., investment). Notice in this problem we are explicitly assuming that there are no capital inflows so the only sources of savings is private savings and government savings.
d. Suppose that the government wants to reduce the deficit and in order to do this the government reduces its expenditures by $100 million. That is, now G=$20. Compute the new equilibrium rate of interest in the loanable funds market. Note: you will need to compute a new equation for SN based on this new government behavior. Assume that nothing has happened to the demand for loanable funds curve you were provided (the investment demand curve in (b)) and that everything else in (b) continues to be true except for the described change in government expenditures. Note this problem still assumes that capital inflows are equal to zero. Explain the result you calculate. 'e. Suppose that the only thing that changes in the problem you were given in (b) is that taxes increase by $10 million to a total of $90 million. What happens to the equilibrium interest rate in the loanable funds market? Illustrate your answer by providing a proof of your results (this will require you to use the equations for private savings, government savings, and national savings!) as well as an explanation. Make sure you provide both proof AND explanation.