Questions:
Coordinate system to find slope of a line
1. Find the slope of the line passing through the points (-8, -3) and (-2, 2).
A) - 5/6
B) - 6/5
C) 5/6
D) 6/5
2. Give the coordinates of the point graphed below.
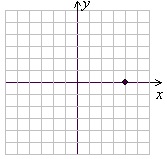
A) (4, 0)
B) (-4, 0)
C) (0, 4)
D) (0, -4)
3. Find the slope of the graphed line.
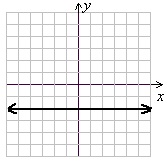
A) Undefined
B) -2
C) 0
D) 1
4. Find the slope of the line passing through the points (4, 0) and (4, 5).
A) Undefined
B) 0
C) 1
D) 5
5. Find the slope of the line passing through the points (-9, -4) and (0, -4).
A) Undefined
B) 0
C) 1
D) 9
6. Graph using the intercept method: 5x - y = 5.
7. Graph using the intercept method: x + 3y = 6.
8. Graph y = 3x.
9. Determine which two equations represent parallel lines.
(a) y = 5/3 x + 4
(b) y = - 3/5 x - 7
(c) y = 2x + 8
(d) y = 2x - 4
A) (c) and (d)
B) (a) and (b)
C) (b) and (c)
D) (a) and (d)
10. Write the equation of the line with slope -2 and y-intercept (0, 0).
11. Find the y-intercept.
-x + 3y = 15
A) (5, 0)
B) (0, -15)
C) (0, 5)
D) (-15, 0)
12. Write the equation of the line passing through (4, 4) and (4, 2).
A) y = 4
B) y = -2x
C) x = 4
D) y = x + 4
13. Write the equation of the line which has y-intercept (0, 5) and is perpendicular to the line with equation y = -3x + 1.
A) y = 3x + 5
B) y = - 1/3 x + 5
C) y = 1/3 x + 5
D) y = -3x + 5
14. Given ƒ(x) = 5x2 - 3x + 1, find ƒ (-2).
A) 15
B) 27
C) -13
D) -25
15. Rewrite the equation 2x - 3y = -6 as a function of x
A) ƒ(x) = 3/2x -6
C) ƒ(x) = 2/3x + 6
B) ƒ(x) = 3/2x - 3
D) ƒ(x) = 2/3 x + 2
16. Graph the inequality.
y < -4
17. Find the slope of any line parallel to the line through points (15, 1) and (4, 2).
18. Rewrite the equation 4x - 6y = -30 as a function of x.
19. Write the equation of the line passing through (3, -7) and (-6, -7).
20. Write the equation of the line that passes through point (-2, 3) with a slope of -4.