Problems:
Write the word or phrase that best completes each statement or answers the question.
Provide an appropriate response.
1) Explain the result if the simplex tableau is solved using a quotient other than the smallest non-negative quotient.
2) Explain why a different slack variable must be used for each constraint when converting constraints to linear equations.
3) When would the simplex method be used instead of the graphical method?
4) Each solution of a simplex tableau corresponds to
5) What happens if an indicator other than the most negative one is chosen to solve a simplex tableau?
6) A negative number in the rightmost column of a simplex tableau tells you that you have made what kind of error when pivoting?
7) No unique optimum solution found from a simplex tableau corresponds to
8) You are given the following linear programming problem (P):
Minimize z = x1 + x2
subject to: -4x1 + 4x2≤1
xl 3x2≤2
x1≥0,x2≥0
9. The dual of (P) is (D). Which of the following statements are true?
a. (P) has no feasible solution and the objective function of (D) is unbounded.
b. (D) has no feasible solution and the objective function of (P) is unbounded.
c. The objective functions of both (P) and (iD) are unbounded.
d. Both (P) and(D) have optimal solutions.
e. Neither (P) nor (D) has feasible solutions.
MULTiPLE CHOiCE. Choose the one alternative that best completes the statement or answers the question.
10. The initial tableau of a linear programming problem is given. Use the simplex method to solve the problem
11. A toy making company has at least 300 squares of felt, 700 oz of stuffing, and 230 ft of trim to make dogs and dinosaurs. A dog uses i square of felt, 4 oz of stuffing, and i ft of trim. A dinosaur uses 2 squares of felt, 3 oz of stuffing, and i ft of trim.
i0) 
it costs the company $i.75 to make each dog and $i.9i for each dinosaur. What is the company's
Minimum cost?
A) $366 B) $350 C) $287 D) $326
12. Pivot once about the circled element in the simplex tableau, and read the solution from the result.
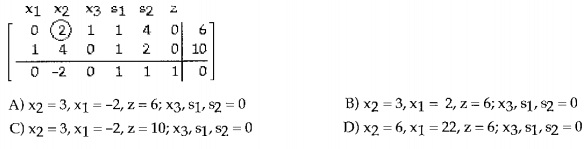
13. A toy making company has at least 300 squares of felt, 700 oz of stuffing, and 230 ft of trim to make dogs and dinosaurs. A dog uses i square of felt, 4 oz of stuffing, and i ft of trim. A dinosaur uses 2 squares of felt, 3 oz of stuffing, and i ft of trim.
14) it costs the company $i.i0 to make each dog and $i.32 for each dinosaur. The company wants to
minimize its costs. What are the coefficients of the constraint inequality for felt?
A) 1,2 i3) 1.10, 1.32 C) 4,3 D) 1,1
15. Find the transpose of the matrix.
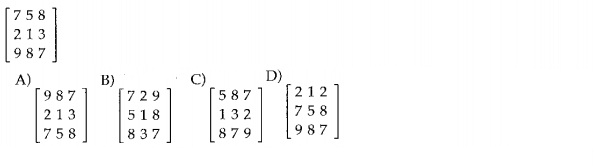
16. Pivot once about the circled element in the simplex tableau, and read the solution from the result
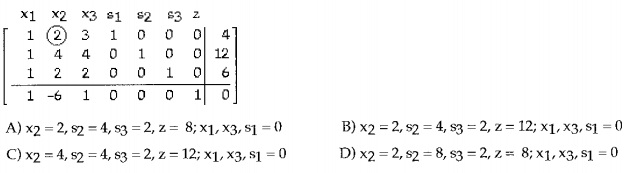
17. Use the simplex method to solve the linear programming problem
Minimize w = 5y1+3y2
Subject to: 2y1+3y2≥9
2y1+y2≥11
y1≥0,y2≥0
A. 27.5 when y1 = 5.5 and y2 = 0
B. 27 when y1 = 5 and y2 = 1
C. 33 when y1 = 11 and y2 = 0
D. 25 when y1 = 2 and y2 = 55
18. Introduce slack variables as necessary, and Write the initial simplex tableau for the problem.
19. ReWrite the objective function into a maximization funtion.
Minimize w = y1+y2+5y3
Subject to: y1+y3≥30
y1+2y2+3y3≥46
2y1+3y2+2y3≥75
y1≥0,y2≥0.y3≥0
A. Maximnize Z = X1+X2+5X3-X4
B. maximize Z = -x1-x3≤30
C. Maximize Z = X1-2X2-3X3≤46
D. Maximize Z = -x1-x2-5x3
20. The initial tableau of a linear programming problem is given. Use the simplex method to solve the problem.
Solve using artificial variables.
Maximize z = 4x1+6x2
subject to: 2x1 + x2 =12
2x1+ 2x2≥20
2x1+2x2≤24
x1≥0,x2≥0
A. Maximum is 72 for x1 = 0, x2 = 12
B. Maximum is 48 for x1 = 12, x2 = 0
C.Maximum is 68 for x1 = 2, x2 = i0
D.Maximum is 56 for x1 = 2, x2 = 8
Minimize w = xl + 2x2
subject to: 2x1+ x2 = 18
2x1+ 2x2≥i7
x1+ x2≤9
x1≥0,x2≥0
A.Minimum is 9 for x1 = 9, x2 = 0
B.Minimum is 9 for x1 = 0, x2 = 9
C.Minimum is i2 for x1 = 8, x2 = 2
D.Minimum is 36 for x1 = 0, x2 = 18