Problems:
Geometry: Incidence geometry
1. Construct a model of incidence geometry that has neither the elliptic hyperbolic nor Euclidean parallel properties.
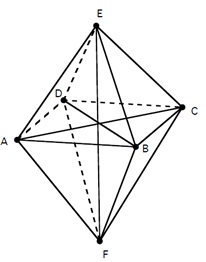
2. Consider a finite geometry where the points are interpreted to be the six vertices of a regular octedron and the lines are sets of exactly two points.
3. Given three collinear points A, B, and C, with B between A and C. Let P be a fourth point on the same line. Show that if B is not between A and P, then C is not between A and P.
4. Let A and B be two points such that point A lies on line I and B∉I. Show that if C∈ AB-, C ≠ A,B, then B and C are on the same side of I.
5. Let y be a circle in the Euclidean plane with center 0 and let A and B be two points on γ. The segment AB is called a chord of γ: let M be its midpoint. If 0≠ M, show that the line through 0 and M is perpendicular to segment AB.