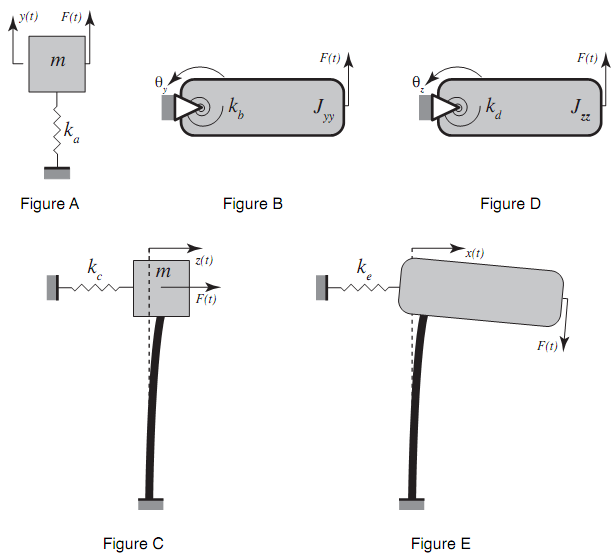
A three-bladed wind turbine has blades that are slightly unbalanced. Recall that the harmonic excitation caused by a rotating unbalance is meΩ2cos(Ωt) in the vertical (y) direction and meΩ2sin(Ωt) in the out-of-plane (z) direction where m = 100 kg is the mass of the rotating unbalance, e = 1 mm is the distance from the center of mass to the center of rotation, and Ω is the rotation speed of the unbalanced mass. The blades are located at a distance R = 1 m from the central vertical (y) axis and rotate at an angular velocity Ω = 5 Hz. The support is a hollow cantilevered steel shaft of height h = 8 m, outer diameter 0.1 m and inner diameter 0.08 m. The mass moments of inertia of the turbine system about the vertical (y) and out of-plane (z) axes are Jyy = Jzz = 100 kg-m2. The total mass of the turbine system is M = 1600 kg. The radius r of the turbine is 0.5m.The support shaft acts as a spring and its compliance allows the turbine to translate along and
rotate about the three axes. These motions will generally be coupled but we will study them independently (as single-degree-of-freedom systems).
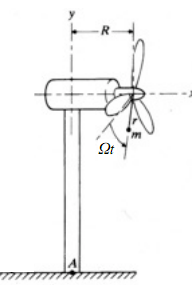
1. Consider just the vertical (y) response of the system when the beam is being stretched. Show that the spring constant, ka, is approximately 70.6 mN/m. What is the steady state amplitude of the vertical response? See Figure A below for an engineering model.
2. Consider just the rotational response of the system about the vertical (y) axis so that the beam is being twisted. Show that the spring constant, kb, is approximately 57.9 kN-m What is the steady state amplitude of this rotational response? See Figure B below.
3. Consider just the translational response in the out-of-plane (z) direction. In this case the support shaft is being bent as a cantilevered beam. Show that the spring, kc, shown in Figure C has a stiffness of approximately 3.4 kN/m. What is the steady state amplitude of this translational response?
4. Consider just the rotational response of the system about the out-of-plane (z) axis so that the beam is again cantilevered but only rotational inertia of the turbine is considered. The unbalanced load creates a moment about the free end of the shaft. This moment changes the slope of the end of the shaft and the shaft acts as a torsional spring with con-stant kd as shown in Figure D. (See the attached notes.) Show that this spring constant is approximately 72.5 kN-m. What is the steady state amplitude of this rotational response?
5. Consider just the translational response in the horizontal (x) direction. The moment gen-erated by the unbalanced load also causes the free end of the shaft (and the turbine) to translate. The shaft can then be modeled as a translational spring as shown in Figure E. The spring stiffness is 3EI/h3, the effective mass is m(1+r/h) and the amplitude of the excitation is 3meRΩ2/2h. (See the attached notes.) What is the steady state amplitude of this translational response?
6. As the blades are spun up to or slowed from the steady operating condition of 5 Hz, what speeds will excite resonances. In each case, what would be the amplitude of response if the blade where left to run at this speed?