Assignment
1. Let G be the following graph:
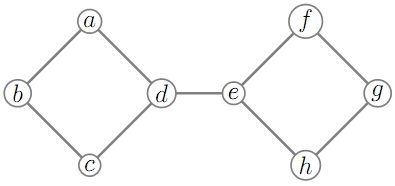
a) Determine the chromatic polynomial of G.
b) Determine the number of proper colourings of K3 + G with 5 colours.
2. Let G be a connected, self-complementary planar graph of order n and size m having four vertices of degree two and the remaining vertices of degree d. If six faces of G are triangles and the remaining faces are pentagons, compute the values of d, n and m. (We do not accept the answer from a drawing, you have to get it through a sequence of logical steps. )
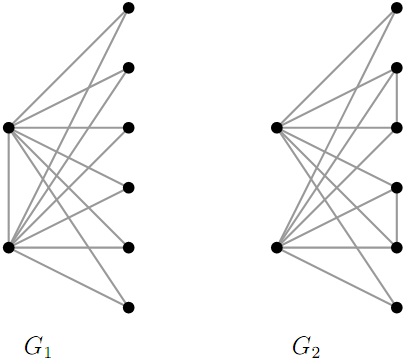
3. Which of the following graphs is closest to being bipartite? Make the corres- ponding calculations and argue your answer.
4. Let G be a graph whose adjacency matrix is in the attached file. Compute the subgraph centraliy and the eigenvector centrality of each node and explain what the results mean.
5. Let A be the adjacency matrix of a connected graph G. Give a formula, in terms of the entries of the powers of A, for the measure of centrality that allows us to make a ranking of the nodes of G from each one of the following criteria:
(a) The degree of each vertex.
(b) The number of triangles in which each vertex participates.
(c)The number of paths of length two starting at each vertex.
(d) The number of paths of length two in which each vertex is the central one.
(e)The number of squares in which each vertex participates.
Format your assignment according to the following formatting requirements:
1. The answer should be typed, double spaced, using Times New Roman font (size 12), with one-inch margins on all sides.
2. The response also include a cover page containing the title of the assignment, the student's name, the course title, and the date. The cover page is not included in the required page length.
3. Also Include a reference page. The Citations and references should follow APA format. The reference page is not included in the required page length.