Compute the products using the row vector rule

Question

Problems:

Compute the products using the row vector rule for computing Ax. If a product is undefined, explain why.

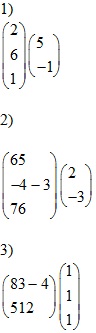
4) let A = [²_-6 ^-1₃] and b =[^b₁^b₂]  .  Show that the equation Ax=b does not have a solution for all possible b, and describe the set of all b for which Ax=b does have a solution.

5) How many rows of A contain a pivot position? Does the equation Ax=b have a solution for each b in R?

Make appropriate calculations and justify your answers and mention an appropriate theorem.

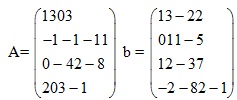
6) Do the columns of B span R⁴R? Does the equation Bx=y have a solution for each y in R⁴ .

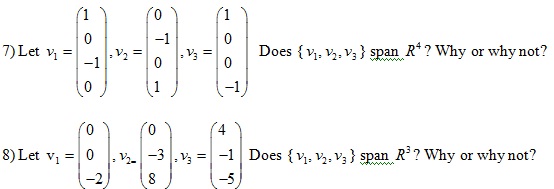
9) True or False

a) the equation Ax=b is referred to as a vector equation.
b) A vector b is a linear combination of t he columns of a matrix A if and only if the equation Ax=b has at least one solution.
c) The equation Ax=b is consistent if the augmented matrix {A b} has a pivot position in every row.
d) The first entry in the product Ax is a sum of products.
e) If the columns of an mxn matrix A span , then the equation Ax=b is consistent for each b in .
f) If A is a m x n matrix and if the equation Ax=b is inconsistent for some b in , then A cannot have a pivot in every row.

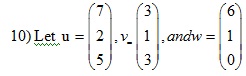
It can be shown that 3u-5v-w=0. Use the fact (and no row operations) to find that satisfy the equation

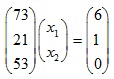
11) Construct a 3x3 matrix, not in echelon form, whose columns span . Show that the matrix you construct has the desired property.

12) Could a set of 3 vectors in span all of ? Explain. What about n vectors in when m is less than n?