Compute the gravitational binding energy

Question

Assignment:

Problems:

1. In this problem we will make a crude estimate of how the luminosity variation of a pulsating star is related to the variation in its radius. This provides a way of estimating the amount by which the radius is changing for a star that we observe to pulse. We will consider a star whose unperturbed state consists of a luminosity L_o, a radius R_o, and a surface temperature T_o.

a) The star's luminosity is related to its radius and surface temperature by L= 4πR²σT⁴. Suppose that, as a result of pulsation, the radius changes by an amount δR and the surface temperature changes by an amount δT. Estimate the resulting change in luminosity δL. You may assume that δR, δT, and δL are all small, so the equations can be linearized.

b) Assume that the star is composed of an adiabatic, ideal gas with adiabatic with adiabatic exponent y, and that the expansion and contraction of the star are homologous. Using these assumptions, derive a relationship between δR and δT.

c) Use the result of part (b) to eliminate δT from your answer to part (a), and arrive at an estimate for the relationship between δL and δR. Based on this result, does the peak luminosity of a pulsating star with y = 5/3 occur when its radius is at its maximum value or its minimum value?

2. We can make a rough estimate of how much the envelope of a red giant should expand as a result of the contraction of its core based on conservation of energy. We will consider a star of mass M and initial radius R, with a core of mass M_c and radius R_c . We will focus on the phase when there are no nuclear reactions in the helium core, and when hydrogen burning in the shell above it either does not occur or occurs too slowly to make a significant contribution to the energy budget.

a) Compute the gravitational binding energy and the total energy of the core, assuming that the electrons are non-relativistic and that radiation pressure is insignificant. Your answer will involve a constant of order unity the depends on the density distribution within the core, which you can simply write as at.

b) Compute the gravitational binding energy and the total energy of the envelope by itself. Again, you will have a constant of order unity, which you can write as α_ce. You may neglect changes in the structure of the envelope due to the gravitational pull of the core.

c) Compute the potential energy associated with gravitational attraction between the core and the envelope, assuming R >> R_c. This will involve yet another constant α_ce.

d) Now suppose that the core contracts from its initial radius R_c,o to a smaller radius R_c,1. This causes the envelope to expand from its initial radius R_o to a new radius R₁. Assuming that the total energy content of the star is conserved in the process, compute R₁/R₀ in terms of R_o,R_c,o, R_c,1, M_c, and M. For numerical convenience, you may set all the α factors equal to 1.

e) Evaluate the ratio of the new and old radii, R₁/R_o. for a core near the Shoenberg-Chandrasekhar limit M_c/M ≈ 0.1 with an initial radius R_c,o/R_c = 0.02 that shrinks by a factor of 2, so that R_c,1/R_o = 0.01.

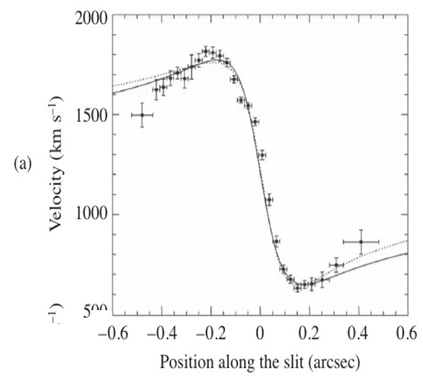
3. The figure shows the rotation curve for the galaxy M87. which is at a distance d = 16 Mpc. Just outside 0.15 aresec from the centre. the rotation curve is approximately Keplerian. Estimate the mass inside this region.