Problem 1. Use the figure below to answer this question. In the figure the location of line 2 is meant to be ambiguous-you must actually figure out its location from the given information! Show your work in order to get full credit.
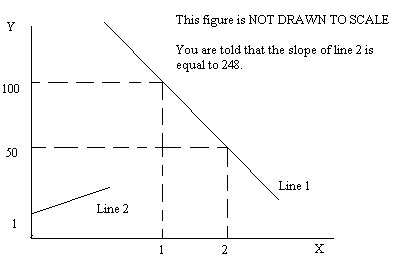
a. Write an equation in slope intercept form for Line 1.
b. Write an equation in slope intercept form for Line 2.
c. Give the coordinates (X, Y) for the point where Line 1 intersects Line 2.
Problem 2. Joe and Marge each produce basketballs and doughnuts. The table below expresses how many hours it takes for each of them to produce 1 basketball or 1 dozen doughnuts. For this problem assume they each have forty hours each week to devote to the production of basketballs and/or doughnuts. Assume that both of their production possibility frontiers are linear.
Hours of Labor to Produce Hours of Labor to Produce One
One Basketball Dozen Doughnuts
Joe 4 hours 1 hour
Marge 2.5 hours 2 hours
a) In the space below draw two separate graphs. In the first graph (label this Joe’s PPF) draw Joe’s PPF measuring basketballs on the horizontal axis and dozens of doughnuts on the vertical axis. Label the x-axis intercept as well as the y-axis intercept. Repeat this for the second graph for Marge’s PPF. Label these graphs clearly and completely to get full credit.
b) Compare the opportunity cost of producing one dozen doughnuts for these two individuals. Who has the lower opportunity cost for producing one dozen doughnuts? (Provide numerical measures with appropriate units of measurement in your answer.)
c) Provide the range of trading prices in terms of dozens of doughnuts that 20 basketballs will trade for given the above information
Problem 3. For each of the following scenarios draw a graph to illustrate the initial situation and the situation after the scenario. Then provide a verbal explanation of what will happen to price and quantity given the scenario. Mark the initial curves and points as D1, S1, P1, and Q1. Mark the final curves and points as D2, S2, P2, and Q2.
a. The market for gasoline-powered cars is initially in equilibrium. The price of gasoline rises due to political upheavals in the oil producing regions of the world. Holding everything else constant, depict the effect of this scenario on the market for gasoline-powered cars and provide a verbal explanation of these effects as well.
b. The cookie market is initially in equilibrium. Suppose the price of sugar, an ingredient in cookies, increases while at the same time people’s incomes increase. Holding everything else constant, depict the effect of these changes on the market for cookies and provide a verbal explanation of these effects as well.
Problem 4. Suppose a market is composed of two consumers, George and Martha. George’s demand for the product is given by the equation P = 100 – Q while Martha’s demand for the product is given by the equation P = 50 – 4Q. Find the market demand curve. If the demand curve has more than one segment, write the equations as well as the relevant ranges for all the segments of the demand curve.