Problem 1. Consider an economy that consists of two consumers and one firm. The firm produces goods using machines and oil. In contrast, consumers consume cheeseballs and television sets. Use the aggregate data below (and Excel) to answer the following questions:
Data:
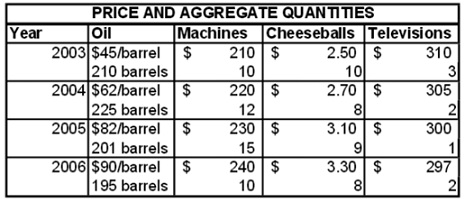
a. Construct a Consumer Price Index for each year of the sample using 2003 as the base year. In doing so, be explicit as to what your mark et basket is (i.e., the market basket of the “typical”or “av erage” consumer). For the sake of this example you will assume that each consumer ends up consuming half of the total production.
b. Construct a CPI using 2006 as base year. To do this you will need to construct another market basket for the “average” consumer using the production figures from 2006.
c. Appended to the same table report no minal GDP, real GDP using 2006 as the base year, and the associated GDP deflat or (calculate each se ries for all years in the sample). Recall from the class discussion that nominal GDP uses current prices and curren t quantities, while real GDP uses prices from the base year and quantities from the current year.
d. Using your answer in parts (b) a nd (c) fill in the following table:
Time Period Inflation using CPI Inflation using GDP deflator
2003-2004
2004-2005
2005-2006
e. Examine your data from (d). Which measure gives a higher value for inflation? Explain. (In particular, if your answer is different from what you think the book would say it “should” be, th en think about what is going on in this case.
Hint: Think about who consumes oil in our model world.)
Problem 2. Consider an economy with one firm that produces widgets using the following production function:
Y=AKα L1- α, where A represents the fixed level of technology. The firm operates in a competitive market and therefore takes factor prices as given. In particular, it takes the wage rate, W, and the rental rate of capital, R, as fixed. In addition, the price of widgets is P.
a. Write down an expression for firm profits as a function of K and L.
b. Derive two expressions (equations) which K and L must satisfy if the firm is behaving optimally (i.e., maximizing prof its). You can do this either using Calculus, as we did in section, or usi ng a heuristic argument, as we did in class. (A “heuristic” argument is one that is not tec hnically rigorous, but conveys the essential intuition.)
c. The parameter α in the Cobb-Douglass technology function is sometimes referred to as representing “capital’s income share in production”. Rearrange one of the two expressions that you derive d in part b to explain why this is an appropriate when to think about this parameter when this is the case.
Problem 3. Consider an economy with a ggregate production function Y = AK0.5L0.5 . Consumption is given by the equation C = 500 + 0.5(Y-T). Invest ment (I) is given by the equation I = 2000 - 100r, where r is the real interest rate in percent. Government spending (G) is 1,000 and taxes (T) is also 1,000. The supply of capital is fixed at 10, the supply of labor is fixed at 10, and the technology level (A) is 50. Consider the effect of a t echnological innovation that changes the investment function to I = 3,000 – 100r.
a. Does investment rise, fall or stay the same?
b. Does the real interest rate rise, fall or stay the same?
c. If the real interest rate changed in part b, by how much did it change?