Problem 1. Which of the following is not a characteristic of normal indifference curves (ICs)?
A. ICs for different levels of utility can never intersect.
B. ICs are downward sloping.
C. The slope between two points on an IC gives the total utility provided by the combinations of goods at those points.
D. There is an IC through every point, describing utility levels for every possible combination of goods.
E. Each IC represents a different but constant level of satisfaction.
Problem 2. Suppose you have just gotten a new DVD player. You spent all of your money on it, and now you’ve realized that you have no money leftover to buy a DVD to watch. You decide to solve this problem by going to the local used CD/DVD store and trading in some CDs that you no longer listen to very often. The clerk initially says that you need to trade in 4 CDs to get one DVD. You think this is unreasonable, because you are only willing to give up a maximum of 3 CDs for one DVD. What does this say about your preferences?
A. MRSDVD,CD = - 1/3
B. MRSCD,DVD = - 3
C. MUDVD = 1
D. MRSDVD,CD = - 3
E. MUCD = 3
Problem 3. Consider the indifference curve below. What can you conclude about the marginal rates of substitution based on this graph?
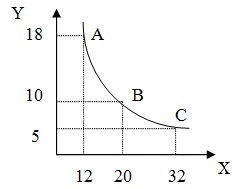
A. MRSXY = -1 from A to B and MRSXY = -5/12 from B to C.
B. MRSXY = -9/10 from A to B and MRSXY = -5/16 from B to C.
C. MRSXY = -1 from A to B and MRSXY = -12/5 from B to C.
D. MRSXY = -3 from A to B and MRSXY = -1/2 from B to C.
E. MRSXY = -10/9 from A to B and MRSXY = -16/5 from B to C.
Problem 4. Halloween is coming up, and Matt (who is too old to trick-or-treat) has decided to buy some candy for himself. The local store has bags of M&Ms ($2 each) and bags of candy corn ($1.50 each), both of which Matt enjoys. However, his budget is limited to $12.
a. Find the equation for Matt’s budget line in slope-intercept form, treating candy corn as the “Y” (vertical axis) good.
b. The following is a graph showing some of Matt’s indifference curves. Draw his budget line on this graph.
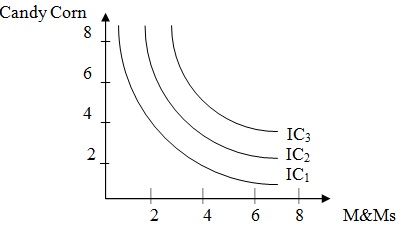
c. Based on the graph above, which indifference curve would Matt most prefer to reach? Can Matt afford to buy enough candy to reach this indifference curve? If not, what is the highest indifference curve he can reach?
d. How much money will Matt spend to consume on the highest indifference curve he can reach? Based on looking at the graph, (roughly) how much of each item will he buy?
Problem 5. By knowing what bundle maximizes an individual’s utility under various price conditions, we can derive a demand curve for that person. Consider the following setup:
Situation 1: Income = $20, Px = $5, Py = $2
Situation 2: Income = $20, Px = $2, Py = $2
a. Draw the budget lines for both situations on one graph, labeling them BL1 and BL2.
b. Suppose we are told something about the consumer’s preferences: in situation 1 she buys X=2 and Y=5, and in situation 2 she buys X=4 and Y=6. Mark and label these points on the appropriate budget lines, and sketch the indifference curve that the consumer reaches in each of the two situations.
c. Set up a new graph, with “Price of X” on the vertical axis and “Quantity of X” on the horizontal axis. For each of the two prices of X that we have considered, plot the price against the quantity demanded at that price (which you can see on the previous graph). Finally, sketch a line through the points and label it “Demand for X.”
d. For extra practice, try assuming that the price of Y changes instead of the price of X. Suppose the new situation has price levels Px = $5 and Py = $5 (this is our new “situation 2”). In this case, the individual consumes X=1 and Y=3. Using this information, along with the information provided for situation1, derive the demand curve for Y.