Assignment:
Q1. Evaluate the following indefinite integrals:
1. ∫ 1/x2 dx
2. ∫ e −xdx
3. ∫ sin(t) cos(t)dt
4. ∫ √s ds
Q2. On a dark night in 1915, a German zeppelin bomber drifts menacingly over London. The men on the ground train a spotlight on the airship, which is traveling at 90 km/hour, and at a constant altitude of 1 km. The beam of the spotlight makes an angle θ with the ground.
1. Draw a diagram of the situation.
2. When the airship is 3 kilometers from the spotlight, how fast is θ changing?
Q3. An electrical circuit consists of two parallel resistors, with resistances R1 and R2 respectively. The total resistance R of the circuit (measured in Ohms ?) is specified by
1/R = 1/ R1 + 1/R2
The resistors are heating up, so their resistances are increasing over time. Suppose that R1 is increasing at a rate of 0.3?/s and R2 is increasing at a rate of 0.2?/s. When R1 = 80? and R2 = 100?, how fast is the total resistance increasing?
Q4. The ideal gas law states that the pressure P, volume V , and temperature T of a gas are related by
P V = N kT
where N is the number of molecules of gas, and k is Bolzmann’s constant, about 1.38 x 10−23J/K where J is Joules and K is Kelvins. Say that I have 1024 molecules of gas. The gas begins at a pressure of 200 kPa, inside a 100 cm3 container, and at a temperature of 400K.
1. Say that I hold the temperature fixed at 400K and begin to decrease the volume of the container at a rate of 10 cm3/s. At what rate is the pressure changing?
2. What if instead the pressure is kept fixed at 200 kPa, and the gas is cooled at a rate of −2K/s. At what rate is the volume changing?
Q5. Use the fundamental theorem of calculus to evaluate ∫ π0 sin(x)dx. You must show your work.
Q6. What is d/dx ∫ x0exp(sin(s) + ss)ds? (Hint: use the fundamental theorem of calculus.)
Q7. Approximate ∫10exp(−t2)dt by partitioning the interval [0, 1] into 5 parts of equal length and sampling exp(−t2) at the midpoint of each part. Round to three decimal places.
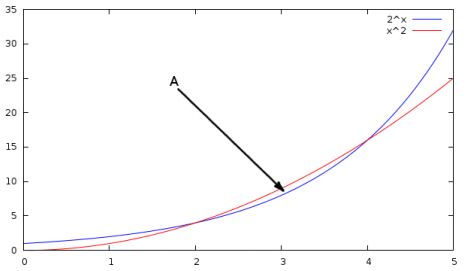
Q8. The graph of 2x crosses the graph of x2 at x = 2 and x = 4; see the diagram below. Given that ∫ 2xdx = (1/ ln(2))2x + C, find the area of the region A enclosed by the two curves.
Provide complete and step by step solution for the question and show calculations and use formulas.