Calculation of location measures and dispersion measures.
Consider the following set of sample data:
78, 121, 143, 88, 110, 107, 62, 122, 130, 95, 78, 139, 89, 135
a) Work out the mean and standard deviation for these sample data.
b) Compute the coefficient of variation for these sample data and interpret its meaning.
Average = 106.9286
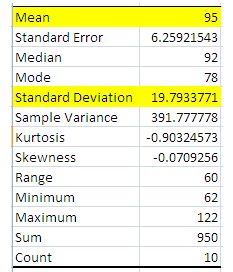
Coefficient = 19.7933771190714 / 106.9286 * 100
Coefficient = 18.5108403251169 %
Coefficient = 18.5% Rounded up = 19%
c) Using Tchebysheff's Theorem, determine the range of values that must include at least 89% of the data. Count the number of data values that fall into this range and comment on whether your interval range was conservative or not.