Calculating electric flux through a disk

Question

Problem 1: Calculating Electric Flux through a Disk: Suppose a disk with area A is placed in a uniform electric field of magnitude E. The disk is oriented so that the vector normal to its surface, n^, makes an angle θ with the electric field, as shown in the figure.

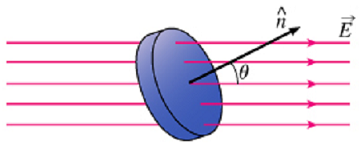
Part A: What is the electric flux φE through the surface of the disk that is facing right (the normal vector to this surface is shown in the figure)? Assume that the presence of the disk does not interfere with the electric field.

Problem 2: The nuclei of large atoms, such as uranium, with 92 protons, can be modeled as spherically symmetric spheres of charge. The radius of the uranium nucleus is approximately 7.4 x 10^-15 m.

Part A: What is the electric field this nucleus produces just outside its surface?

Part B: What magnitude of electric field does it produce at the distance of the electrons, which is about 2.0 × 10^-10 m?

Part C: The electrons can be modeled as forming a uniform shell of negative charge. What net electric field do they produce at the location of the nucleus?

Problem 3: A Conducting Shell around a Conducting Rod: An infinitely long conducting cylindrical rod with a positive charge λ per unit length is surrounded by a conducting cylindrical shell (which is also infinitely long) with a charge per unit length of -2λ and radius r₁, as shown in the figure.

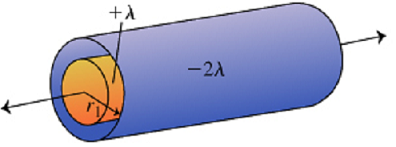
Part A: What is E(r), the radial component of the electric field between the rod and cylindrical shell as a function of the distance r from the axis of the cylindrical rod?

Part B: What is σ_inner, the surface charge density (charge per unit area) on the inner surface of the conducting shell?

Part C: What is σ_outer, the surface charge density on the outside of the conducting shell? (Recall from the problem statement that the conducting shell has a total charge per unit length given by -2λ.)

Part D: What is the radial component of the electric field, E(r), outside the shell?

Problem 4: The Charge inside a Conductor: A spherical cavity is hollowed out of the interior of a neutral conducting sphere. At the center of the cavity is a point charge, of positive charge q.

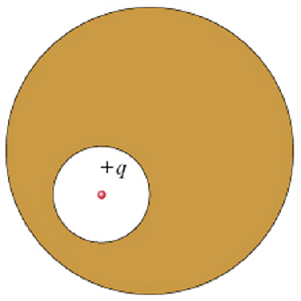
Part A: What is the total surface charge q_int on the interior surface of the conductor (i.e., on the wall of the cavity)?

Part B - What is the magnitude E_int of the electric field inside the cavity as a function of the distance from the point charge? Let k, as usual, denote 1/4π∈₀.

- 0

- kq/r²

- 2kq/r²

Part C: What is the electric field Eext outside the conductor?

- Zero

- The same as the field produced by a point charge q located at the center of the sphere

- The same as the field produced by a point charge located at the position of the charge in the cavity

Now a second charge, q₂, is brought near the outside of the conductor. Which of the following quantities would change?

Part D: The total surface charge on the wall of the cavity, q_int:

- would change

- would not change

Part E: The total surface charge on the exterior of the conductor, q_ext:

- would change

- would not change

Part F: The electric field within the cavity, E_cav:

- would change

- would not change

Part G: The electric field outside the conductor, E_ext:

- would change

- would not change

Question 5: An infinitely long cylindrical conductor has radius R and uniform surface charge density σ.

Part A: In terms of σ and R, what is the charge per unit length λ for the cylinder?

Part B: In terms of σ, what is the magnitude of the electric field produced by the charged cylinder at a distance r > R from its axis?

Part C - Express the result of part B in terms of λ.

Question 6: A hollow, conducting sphere with an outer radius of 0.251 m and an inner radius of 0.201 m has a uniform surface charge density of +6.40 × 10^-6 C/m². A charge of -0.780 μC is now introduced into the cavity inside the sphere.

Part A: What is the new charge density on the outside of the sphere?

Part B: Calculate the strength of the electric field just outside the sphere.

Part C: What is the electric flux through a spherical surface just inside the inner surface of the sphere?

The tutors associated with Gauss Law Assignment Help service are highly skilled and competent and can cover almost all the topics related to the Gauss Law with ease.

Tags: Gauss Law Assignment Help, Gauss Law Homework Help, Gauss Law Coursework, Gauss Law Solved Assignments, Electric Flux Assignment Help, Electric Flux Homework Help, Electric Field Assignment Help, Electric Field Homework Help