Calculating a marginal density

Question

Solve the following problem:

Monte Carlo marginalization is a technique for calculating a marginal density when simulating from a joint density. Let (X_i, Y_i) ∼ f_XY (x, y), independent, and the corresponding marginal distribution f_X(x) = R f_XY (x, y)dy.

a. Let w(x) be an arbitrary density. Show that

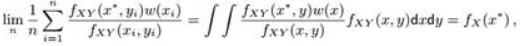
which provides a Monte Carlo estimate of fX, the marginal distribution of X, when the joint distribution is only known up to a constant.

b. Let X|Y = y ∼ G(y, 1) and Y ∼ Exp(1). Use the technique above to plot the marginal density of X. Compare this with the exact marginal.

c. Show that choosing w(x) = fX(x) works to produce the marginal distribution and that it is optimal in the sense of the variance of the resulting estimator.